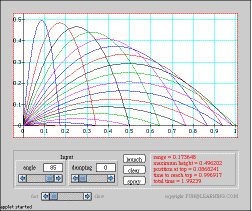
This applet allows the user to set the launch angle and coefficient of linear air resistance. It then animates the trajectory of the body and calculates some of its properties numerically.

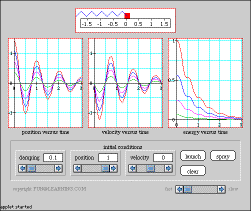This applet allows the user to set the damping coefficient and initial position and velocity. It then animates the motion of the oscillator and plots its position,velocity, and energy as functions of time.

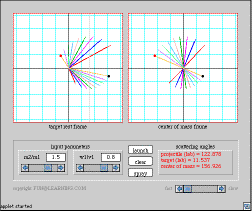This applet animates elastic collisions of two point masses. The user enters the ratio of the target mass to the projectile mass and the ratio of the projectile's final speed to its initial speed, and the applet animates the collision in the target rest frame and in the center of mass frame.

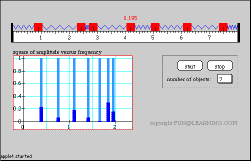The user sets the initial positions of the bodies either by sliding them along the track or by clicking on one of the light blue bars in the frequency spectrum, which puts the system into its corresponding normal mode. The frequency spectrum of the resulting motion is shown by the dark blue bars. The number of bodies can be varied from 1 to 7.

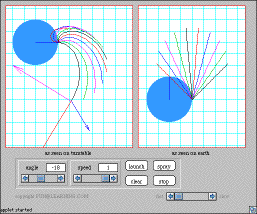A kid riding around on a turntable throws a ball horizontally, and the applet shows top views of its trajectory as seen from the turntable and from the earth. Also shown are the ball's velocity (red), the centrifugal force (blue), and the coriolis force (magenta). The user can vary the speed and angle at which the kid throws the ball.

This applet allows the user to set the relative energy of two bodies. It then animates the motion in the rest frame of one of the bodies and in the effective potential diagram, and calculates some of the properties of the orbit numerically.

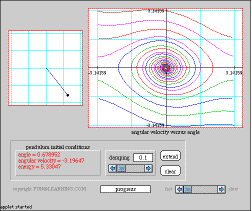This applet allows the user to set the damping and initial angle and angular velocity. It then animates the motion of the pendulum and plots its trajectory in the phase plane.

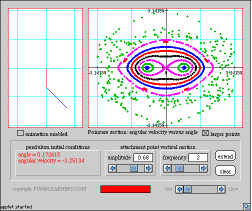This applet allows the user to set the amplitude and frequency of vertical oscillation of the pendulum's attachment point, and the initial angle and angular velocity. It then animates the motion of the pendulum and generates the corresponding Poincaré section.

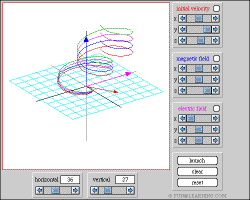This applet allows the user to set the electric and magnetic fields, and the initial velocity of the charged particle. It then animates the motion of the particle.

This applet animates the motion of a particle in the Henon-Heiles potential and generates the corresponding Poincaré section.