
Two Cars in
2-Dimensional Collision
Inelastic
Collision
A GIF Animation
Collisions between objects are governed by laws of momentum and
energy. When a collision occurs in an isolated system, the total
momentum of the system of objects is conserved. Provided that there
are no net external forces acting upon the objects, the momentum of
all objects before the collision equals the momentum of all objects
after the collision. If there are only two objects involved in the
collision, then the momentum change of the individual objects are
equal in magnitude and opposite in direction.
Certain collisions are referred to as elastic collisions. Elastic
collisions are collisions in which both momentum and kinetic energy
are conserved. The total system kinetic energy before the collision
equals the total system kinetic energy after the collision. If total
kinetic energy is not conserved, then the collision is referred to as
an inelastic collision.
The animation below portrays the
inelastic collision between two
1000-kg cars. The before- and after-collision velocities and momentum
are shown in the data tables.
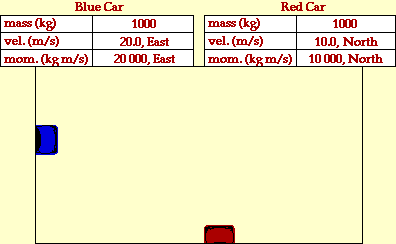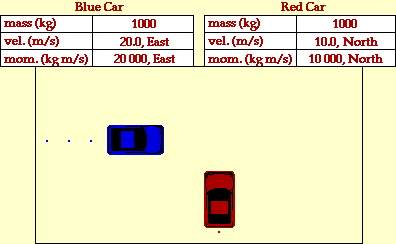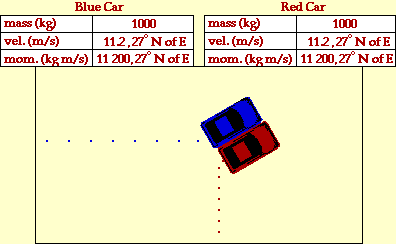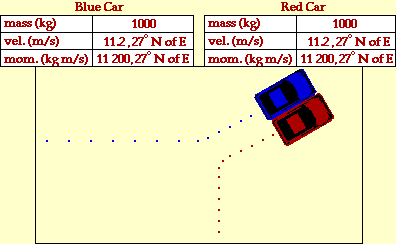
In the collision between the two cars, total system momentum is
conserved. Yet this might not be apparent without an understanding of
the vector nature of momentum. Momenum, like all vector quantities,
has both a magnitude (size) and a direction. When considering
the total momentum of the system before the collision, the individual
momentum of the two cars must be added as vectors. That is, 20 000
kg*m/s, East must be added to 10 000 kg*m/s, North. The sum of these
two vectors is not 30 000 kg*m/s; this would only be the case if the
two momentum vectors had the same direction. Instead, the sum of 20
000 kg*m/s, East and 10 000 kg*m/s, North is 22 361 kg*m/s at an
angle of 26.6 North of East. Since the two momentum vectors are at
right angles, their sum can be found using the Pythagorean theorem;
the direction can be found using SOH CAH TOA (specifically, the
tangent function). The value 22 361 kg*m/s is the total momentum of
the system before the collision; and since momentum is conserved, it
is also the total momentum of the system after the collision. In
order to determine the momentum of either individual car, this total
system momentum must be divided by two (approx. 11 200 kg*m/s). Once
the momentum of the individual cars are known, the after-collision
velocity is determined by simply dividing momentum by mass (v=p/m).
An analysis of the kinetic energy of the two objects reveals that
the total system kinetic energy before the collision is 250 000
Joules (200 000 J for the eastbound car plus 50 000 J for the
northbound car). After the collision, the total system kinetic energy
is 125 000 Joules (62 500 J for each car). The total kinetic energy
before the collision is not equal to the total kinetic energy
after the collision. A large portion of the kinetic energy is
converted to other forms of energy such as sound energy and thermal
energy. A collision in which total system kinetic energy is
not conserved is known as an inelastic collision.
For more information on physical descriptions of motion,
visit
The
Physics Classroom. Specific information is available there on the
following topics:
This page was created by
Tom
Henderson of
Glenbrook South
High School.
Comments and suggestions can be sent by e-mail to
Tom
Henderson.
A hearty thanks is due to lab assistant Bryce Mautner for her
assistance with the graphics and GIF animation.
This page last updated on 4/8/97.
