The Diesel and Freight
Car
Inelastic Collision
A GIF Animation
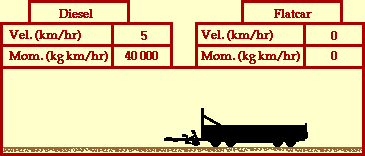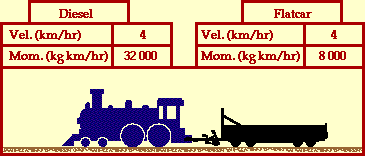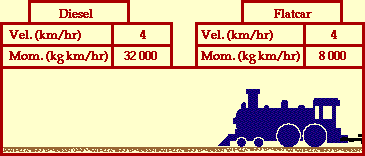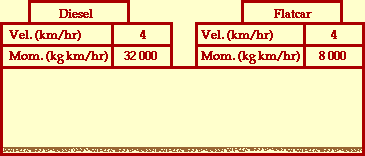
The animation below portrays the inelastic collision between a very massive diesel and a less massive flatcar. Before the collision, the diesel is in motion with a velocity of 5 km/hr and the flatcar is at rest. The mass of the diesel is 8000 kg and the mass of the flatcar is 2000 kg. The diesel has four times the mass of the freight car. After the collision, both the diesel and the flatcar move together with the same velocity. (Collisions such as this where the two objects stick together and move with the same post-collision velocity are referred to as inelastic collisions.) What is the after-collision velocity of the two railroad cars?
Collisions between objects are governed by laws of momentum and energy. When a collision occurs in an isolated system, the total momentum of the system of objects is conserved. Provided that there are no net external forces acting upon the two cars, the momentum of the diesel and the flatcar before the collision equals the momentum of the diesel and the flatcar after the collision
The mathematics of this problem is simplified by the fact that before the collision, there is only one object in motion and after the collision both objects have the same velocity. That is to say, a momentum analysis would show that all the momentum was concentrated in the diesel before the collision. And after the collision, all the momentum was the result of a single object (the combination of the diesel and flatcar) moving at an easily predictable velocity.
The prediction of the final velocity of the two cars involves determining the ratio by which the mass which is in motion changed; and then dividing the initial velocity by that ratio. That is if the amount of mass in motion increases by a factor of two, then the velocity would decrease by a factor of two (divid the original velocity by two). If the amount of mass in motion increases by a factor of five, then the velocity would decrease by a factor of five (divide the original velocity by five). In the case of the animation above, the amount of mass in motion increased by a factor of 5/4; a change from say 8000 kg for the diesel before the collision to 10 000 kg for the combination of the diesel and flatcar after the collision. Since the amount of mass in motion increased by a factor of 5/4, the velocity at which that mass is in motion must decrease by a factor of 5/4. That is, the original velocity of 5 km/hr must be divided by 5/4. Voila! The result is 4 km/hr; the diesel and flatcar move together with a velocity of 4 km/hr after the collision.
For more information on physical descriptions of motion,
visit
The
Physics Classroom. Specific information is available there on the
following topics:
Other animations can be seen at the Multimedia Physics Studios. Other useful resources regarding the physics of motion is available through the Glenbrook South Physics Home Page.
This page was created by
Tom
Henderson of
Glenbrook South
High School.
Comments and suggestions can be sent by e-mail to
Tom
Henderson.
A hearty thanks is due to lab assistant Amit Patel for his
assistance with the graphics and GIF animation.
This page last updated on 4/18/97.