Pendule élastique
Principe:
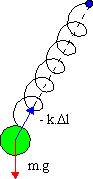 On considère un ressort de raideur k mobile autour d'un axe de rotation.
Une masse m est suspendue au ressort dont la longueur devient l, l'ensemble constitue un "pendule élastique".
On considère un ressort de raideur k mobile autour d'un axe de rotation.
Une masse m est suspendue au ressort dont la longueur devient l, l'ensemble constitue un "pendule élastique".
La masse m est soumise à son poids F1 = mg et à la force de rappel du ressort
F2 = -k.Dl.
On néglige la masse du ressort et tous les frottements. La vitesse initiale est toujours nulle.
On a donc : mg = F1 + F2
En projettant cette équation sur un axe vertical et un axe horizontal, on obtient deux équations
qui sont intégrées par la méthode numérique de Runge-Kutta.
La complexité du mouvement (d'où pendule éthylique dans le menu) résulte
du couplage entre deux pulsations :
celle d'un mouvement pendulaire classique (w2 = l/g)
celle de l'oscillateur harmonique formé par l'association masse-ressort (w2 = k/m).
Si la raideur du ressort est grande, les deux mouvements sont pratiquement découplés.
L’applet :
Pour modifier les conditions initiales :
Cliquer sur le bouton [Arrêt]. Avec la souris, glisser la masse à l'intérieur
du cadre bleu qui s'affiche alors. Le système démarre avec de nouvelles conditions initiales
lorsque l'on relache le bouton de la souris.
Un click sur le bouton [Départ] relance le système avec les valeurs des
dernières conditions initiales utilisées.
On peut aussi modifier la raideur du ressort. (la valeur minimale est égale à 2)
Cas particuliers:
1- Placer la masse à la verticale du point de suspension.
2- Positionner la masse pour annuler la force de rappel dynamique du ressort.
 Retour au menu.
Retour au menu.
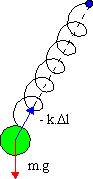 On considère un ressort de raideur k mobile autour d'un axe de rotation.
Une masse m est suspendue au ressort dont la longueur devient l, l'ensemble constitue un "pendule élastique".
On considère un ressort de raideur k mobile autour d'un axe de rotation.
Une masse m est suspendue au ressort dont la longueur devient l, l'ensemble constitue un "pendule élastique".