|
|
|
|
Вычисление пределов функций
Многие функции
при приближении аргумента к некоторому значению или к некоторой области значений
стремятся к определенному пределу. Так, функция sin(x)/x
при х, стремящемся к нулю (обозначим это как х—> 0), дает предел 1 в
виде устранимой неопределенности 0/0.
Численные
математические системы, равно как и большинство программ на обычных языках программирования,
не воспринимают выражение 0/0 —> 1 как объективную реальность. Их защитный
механизм настроен на примитивное правило — ничего нельзя делить на 0. Следовательно,
вычисление sin(x)/x при х = 0 будет сопровождаться выдачей ошибки
типа «Деление на 0». Конечно, в данном конкретном случае можно предусмотреть
особый результат — выдать 1 при х = 0. Но это частный случай. В целом
же подобные системы «не понимают» понятия предела.
Пределом
некоторых функций может быть бесконечность, тогда как многие функции стремятся
к конечному пределу при аргументе х, стремящемся к бесконечности. Система
Mathematica не только численно находит пределы функций, заданных аналитически,
но и позволяет найти предел в виде математического выражения.
На рис. 4.10
представлены примеры применения функции
Limit. Они показывают, что возможно
вычисление пределов функций, устремляющихся к бесконечности, и вычисление пределов
при переменной х, стремящейся в бесконечность. Вычисление пределов функций
в аналитическом виде — важное достоинство систем символьной математики.
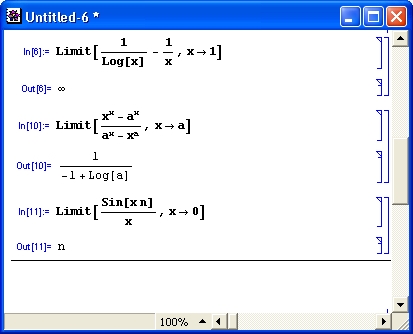
Рис. 4.10. Примеры вычисления пределов
При работе с функцией Limit используются следующие опции:
Применение данных опций поясняют примеры, показанные на рис. 4.11.
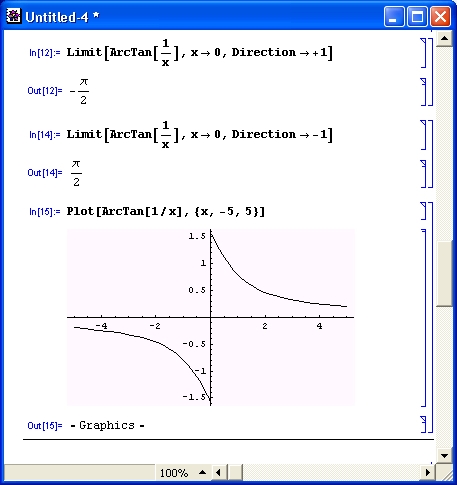
Рис. 4.11. Примеры вычисления пределов с применением опций
|
|
|
|