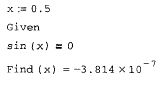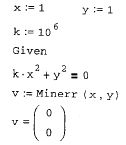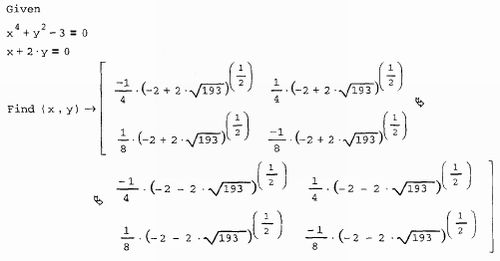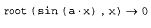• 8.1. Одно уравнение с одним неизвестным
• 8.2. Корни полинома
• 8.3. Системы уравнений
• 8.4. О численных методах решения систем уравнений*
• 8.5. Приближенное решение уравнений
• 8.6. Поиск экстремума функции
  • 8.6.1. Экстремум функции одной переменной
  • 8.6.2. Условный экстремум
  • 8.6.3. Экстремум функции многих переменных
  • 8.6.4. Линейное программирование*
• 8.7. Символьное решение уравнений
• 8.8. Метод продолжения по параметру*

8.1. Одно уравнение с одним неизвестным
Рассмотрим одно алгебраическое уравнение с одним неизвестным х.
f(x}=0, например, sin(x)=0.
Для решения таких уравнений MathCAD имеет встроенную функцию root,которая, в зависимости от типа задачи, может включать либо два, либо че- тыре аргумента и, соответственно, работает несколько по-разному.
- roottf(х),х);
- roottf(х),х,а,Ь);
 f (х) - скалярная функция, определяющая уравнение ;
 х - скалярная переменная, относительно которой решается уравнение;
 а,b - границы интервала, внутри которого происходит поиск корня.
Первый тип функции root требует дополнительного задания начального значения (guess value) переменной х. Для этого нужно просто предварительноприсвоить х некоторое число. Поиск корня будет производиться вблизи
этого числа. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня.
Приведем пример решения очень простого уравнения sin(x)=o, корни которого известны заранее.
Листинг 8.1. Поиск корня нелинейного алгебраического уравнения


Рис. 8.1. Графическоерешение уравнения sin(x)=0
График функции f (x)=sin(x) и положение найденного корня показаны нарис. 8.1. Обратите внимание, что хотя уравнение имеет бесконечное количество корней , MathCAD находит (с заданной точностью) только один из них, х₀, лежащий наиболее близко к х=о.5. Если задать другое начальное значение, например, х=з, то решением будет другойкорень уравнения xi=n и т. д. Таким образом, для поиска корня средствами MathCAD требуется его предварительная локализация. Это связано с особенностями выбранного численного метода, который называется методомсекущих и состоит в следующем (рис. 8.2):
1. Начальное приближение принимается за о-е приближение к корню: хО=х.
2. Выбирается шаг и определяется первое приближение к корню xl=xO+h.
3. Через эти две точки проводится секущая - прямая линия, которая пересекает ось х в некоторой точке х2. Эта точка принимается за второе приближение.
4. Новая секущая проводится через первую и вторую точки, тем самым определяя третье приближение, и т. д.
5. Если на каком-либо шаге оказывается, что уравнение выполнено, т. е.If (x) |<TOL, то итерационный процесс прерывается, и х выдается в качестве решения.

Рис. 8.2. Иллюстрация метода секущих
Результат, показанный на рис. 8.2, получен для погрешности вычислений,которой в целях иллюстративности предварительно присвоено значениетоb=о.5. Поэтому для поиска корня с такой невысокой точностью оказалосьдостаточно одной итерации. В вычислениях, приведенных в листинге 8.1,погрешность TOL=O.OOI была установлена по умолчанию, и решение, выданное численным методом, лежало намного ближе к истинному положениюкорня х=о. Иными словами, чем меньше константа TOL, тем ближе к нулюбудет значение f (х) в найденном корне, но тем больше времени будет затрачено вычислительным процессором MathCAD на его поиск.

Примечание
Соответствующий пример можно найти в Центре Ресурсов. Он расположен вразделе "Solving Equations" (Решение уравнений) и называется "Effects of TOLon Solving Equations" (Влияние константы TOL на решение уравнений).

Если уравнение неразрешимо, то при попытке найти его корень будет выдано сообщение об ошибке. Кроме того, к ошибке или выдаче неправильного корня может привести и попытка применить метод секущих в областилокального максимума или минимума f(x). В этом случае секущая можетиметь направление, близкое к горизонтальному, выводя точку следующегоприближения далеко от предполагаемого положения корня. Для решениятаких уравнений лучше применять другую встроенную функцию Minerr(см. разд. 8.5). Аналогичные проблемы могут возникнуть, если начальноеприближение выбрано слишком далеко от настоящего решения, илиf (х) имеет особенности типа бесконечности.

Примечание
Для решения уравнения с одним неизвестным применимы и градиентные методы, относящиеся в MathCAD к системам уравнений. Информация об этомприведена в разд. 8.3.

Иногда удобнее задавать не начальное приближение к корню, а интервал[а,b], внутри которого корень заведомо находится. В этом случае следуетиспользовать функцию root с четырьмя аргументами, а присваивать начальное значение х не нужно, как показано в листинге 8.2. Поиск корня будетосуществлен в промежутке между а и ь альтернативным численным методом(Риддера или Брента).
Листинг 8.2. Поиск корня алгебраического уравнения в заданном интервале

Обратите внимание, что явный вид функции f (х) может быть определеннепосредственно в теле функции root.
Когда root имеет четыре аргумента, следует помнить о двух ее особенностях:
- внутри интервала [а,ь] не должно находиться более одного корня, иначебудет найден один из них, заранее неизвестно какой именно;
- значения f (а) и f(b) должны иметь разный знак, иначе будет выданосообщение об ошибке.
Если уравнение не имеет действительных корней, но имеет мнимые, то ихтакже можно найти. В листинге 8.3 приведен пример, в котором уравнениех²+1=о, имеющее два чисто мнимых корня, решается два раза с разными начальными значениями. При задании начального значения 0.5 (первая строка листинга) численный метод отыскивает первый корень (отрицательнуюмнимую единицу -i), а при начальном значении -0.5 (третья строка листинга) находится и второй корень (i).
Листинг 8.3. Поиск мнимого корня

Для решения этого уравнения второй вид функции root (с четырьмя, а нес двумя аргументами) неприменим, поскольку f (х) является положительно-определенной, и указать интервал, на границах которого она имела бы разный знак, невозможно.
Остается добавить, что f (х) может быть функцией не только х, а любогоколичества аргументов. Именно поэтому в самой функции root необходимоопределить, относительно какого из аргументов следует решить уравнение.Эта возможность проиллюстрирована листингом 8.4 на примере функциидвух переменных f (х,у)=х²-у²+з. В нем сначала решается уравнениеf (х,0)=о относительно переменной х, а потом - другое уравнение f (i,y)=oотносительно переменной у.
Листинг 8.4. Поиск корня уравнения, заданногофункцией двух переменных

В первой строке листинга определяется функция f(x,y), во второй и третьей - значения, для которых будет производиться решение уравнения по у их соответственно. В четвертой строке решено уравнение f (х,0)=о, а в последней -уравнение f (i,y)=o. He забывайте при численном решении уравнений относительно одной из переменных предварительно определить значения остальных переменных. Иначе попытка вычислить уравнения приведет к появлению ошибки "This variable or function is not defined above", вданном случае говорящей о том, что другая переменная ранее не определена. Конечно, можно указать значение других переменных непосредственновнутри функции root, беспрепятственно удалив, например, вторую и третьюстроки листинга 8.4, и введя его последние строки в виде root(f (x,0) ,х)= иroot (f (1, у), у) =, соответственно.

Примечание
Для того чтобы отыскать зависимость корней уравнения, вычисленных по одной переменной, от других переменных, разработаны специальные эффективные алгоритмы. Об одной из возможностей читайте в разд. 8.8.

8.2. Корни полинома
Если функция f (х) является полиномом, то все его корни можно определить,используя встроенную функцию polyroots(v), где v - вектор, составленный из коэффициентов полинома.
Поскольку полином N-Й степени имеет ровно N корней (некоторые из нихмогут быть кратными), вектор v должен состоять из N+I элемента. Результатом действия функции poiyroots является вектор, составленный из N корнейрассматриваемого полинома. При этом нет надобности вводить какое-либоначальное приближение, как для функции root. Пример поиска корней полинома четвертой степени иллюстрируется листингом 8.5.
Листинг 8.5. Поиск корня полинома

Коэффициенты рассматриваемого в примере полинома f (x) = (x-3)-(x-l)³=x⁴-6x³+12x²-10x+3 записаны в виде вектора в первой строке листинга. Первым в векторе должен идти свободный член полинома, вторым - коэффициент при х¹ и т. д.Соответственно, последним N+I элементом вектора должен быть коэффициент при старшей степени X^N.

Cовет
Иногда исходный полином имеется не в развернутом виде, а, например, какпроизведение нескольких полиномов. В этом случае определить все его коэффициенты можно, выделив его и выбрав в меню Symbolics (Символика) пунктExpand (Разложить). В результате символьный процессор MathCAD сам преобразует полином в нужную форму, пользователю надо будет только корректноввести ее в аргументы функции poiyroots.

Во второй строке листинга 8.5 показано действие функции poiyroots. Обратите внимание, что численный метод вместо двух из трех действительныхединичных корней (иными словами, кратного корня 1) выдает два мнимыхчисла. Однако малая мнимая часть этих корней находится в пределах погрешности, определяемой константой TOL, и не должна вводить пользователей в заблуждение. Просто нужно помнить, что корни полинома могут бытькомплексными, и ошибка вычислений может сказываться как на действительной, так и на комплексной части искомого корня.
Для функции poiyroots можно выбрать один из двух численных методов -метод полиномов Лаггера (он установлен по умолчанию) или метод парнойматрицы.
Для смены метода:
1. Вызовите контекстное меню, щелкнув правой кнопкой мыши на слове polyroots.
2. В верхней части контекстного меню выберите либо пункт LaGuerre(Лаггера), либо Companion Matrix (Парная матрица).
3. Щелкните вне действия функции polyroots - если включен режим автоматических вычислений, будет произведен пересчет корней полинома всоответствии с вновь выбранным методом.
Для того чтобы оставить за MathCAD выбор метода решения, установитефлажок AutoSelect (Автоматический выбор), выбрав одноименный пункт втом же самом контекстном меню.

8.3. Системы уравнений
Рассмотрим решение системы N нелинейных уравнений с м неизвестными
Hекоторые скалярные функции отскалярных переменных и, возможно, от еще каких-либо переменных. Уравнений может быть как больше, так и меньше числа переменных. Заметим, что систему (1) можно формально переписать в виде f(x)=o, где х - вектор, составленный из переменных xi,x₂,... ,х_м, a f (x) - соответствующая векторная функция.
Для решения систем имеется специальный вычислительный блок, состоящийиз трех частей, идущих последовательно друг за другом:- Given - ключевое слово;
- система, записанная логическими операторами в виде равенств и, возможно, неравенств;
- Find (xi,... ,XM) - встроенная функция для решения системы относительно переменных xi,... ,х_м.
Вставлять логические операторы следует, пользуясь панелью инструментовBoolean (Булевы операторы). Если вы предпочитаете ввод с клавиатуры,помните, что логический знак равенства вводится сочетанием клавиш<Ctrl>+<=>. Блок Given/Find использует для поиска решения итерационные методы, поэтому, как и для функции root, требуется задать начальныезначения для всех XI,...,X_M. Сделать это необходимо до ключевого слова Given. Значение функции Find есть вектор, составленный из решения покаждой переменной. Таким образом, число элементов вектора равно числуаргументов Find.В листинге 8.6 приведен пример решения системы двух уравнений.
Листинг 8,6. Решение системы уравнений

В первых двух строках листинга вводятся функции, которые определяютсистему уравнений. Затем переменным х и у, относительно которых онабудет решаться, присваиваются начальные значения. После этого следуетключевое слово Given и два логических оператора, выражающих рассматриваемую систему уравнений. Завершает вычислительный блок функция Find,значение которой присваивается вектору v. Следующая строка показываетсодержание вектора v, т. е. решение системы. Первый элемент вектора естьпервый аргумент функции Find, второй элемент - ее второй аргумент.В последних двух строках осуществлена проверка правильности решенияуравнений.

Сoвeт
Часто бывает очень полезно проверить точность решения уравнений, вычисливзначения образующих их функций в найденных вычислительным процессоромкорнях, как это сделано в конце листинга 8.6.

Отметим, что уравнения можно определить непосредственно внутри вычислительного блока. Таким образом, можно не определять заранее функцииf (х,у) ид(х,у), как это сделано в первых двух строках листинга 8.6, а сразунаписать:
Такая форма представляет уравнения в более привычной и наглядной форме, особенно подходящей для документирования работы.
Графическая интерпретация рассмотренной системы представлена нарис. 8.3. Каждое из уравнений показано на плоскости XY графиком. Первое - сплошной кривой, второе - пунктиром. Поскольку второе уравнениелинейное, то оно определяет на плоскости XY прямую. Две точки пересечения кривых соответствуют одновременному выполнению обоих уравнений,т. е. искомым действительным корням системы. Как нетрудно убедиться,в листинге найдено только одно из двух решений - находящееся в правойнижней части графика. Чтобы отыскать и второе решение, следует повторить вычисления, изменив начальные значения так, чтобы они лежали ближе к другой точке пересечения графиков, например x=-i, y=-i.


Рис. 8.3. Графическоерешение системы двухуравнений
Пока мы рассмотрели пример системы из двух уравнений и таким же числом неизвестных, что встречается наиболее часто. Но число уравнений инеизвестных может и не совпадать. Более того, в вычислительный блокможно добавить дополнительные условия в виде неравенств. Например, введение ограничения на поиск только отрицательных значений х в рассмотренный выше листинг 8.6 приведет к нахождению другого решения, как этопоказано в листинге 8.7.
Листинг 8.7. Решение системы уравнений и неравенств

Обратите внимание, что, несмотря на те же начальные значения, что ив листинге 8.6, мы получили в листинге 8.7 другой корень. Это произошлоименно благодаря введению дополнительного неравенства, которое определено в блоке Given в предпоследней строке листинга 8.7.
Если предпринять попытку решить несовместную систему, MathCAD выдастсообщение об ошибке, гласящее, что ни одного решения не найдено, ипредложение попробовать поменять начальные значения или значение погрешности.

Примечание
Вычислительный блок использует константу CTOL в качестве погрешности выполнения уравнений, введенных после ключевого слова Given. Например^ еслистоь=0.001, то уравнение х=Ю будет считаться выполненным и при х=10.001,и при х=9.999. Другая константа TOL определяет условие прекращения итераций численным алгоритмом (см. разд. 8.4). Значение CTOL может быть задано пользователем также, как и TOL, например, CTOL: =0.01. По умолчанию принято, что CTOL=TOL=O. 001, но вы по желанию можете переопределить их.

Особенную осторожность следует соблюдать при решении систем с числомнеизвестных большим, чем число уравнений. Например, можно удалить одно из двух уравнений из рассмотренного нами листинга 8.6, попытавшисьрешить единственное уравнение д(х,у)=о с двумя неизвестными х и у.В такой постановке задача имеет бесконечное множество корней: для любого х и, соответственно, у=-х/2 условие, определяющее единственное уравнение, выполнено. Однако даже если корней бесконечно много, численныйметод будет производить расчеты только до тех пор, пока логические выражения в вычислительном блоке не будут выполнены (в пределах погрешности). После этого итерации будут остановлены и выдано решение. В результате будет найдена всего одна пара значений (х,у), обнаруженная первой.

Примечание
О том, как найти все решения рассматриваемой задачи, рассказываетсяв разд. 8.7.

Вычислительным блоком с функцией Find можно найти и корень уравненияс одним неизвестным. Действие Find в этом случае совершенно аналогичноуже рассмотренным в данном разделе примерам. Задача поиска корня рассматривается как решение системы, состоящей из одного уравнения. Единственным отличием будет скалярный, а не векторный тип числа, возвращаемого функцией Find. Пример решения уравнения из предыдущего раздела приведен в листинге 8.8.
Листинг 8.8. Поиск корня уравнения с одним неизвестнымс помощью функции Find

В чем же отличие приведенного решения от листинга 8.1 с функцией root ? Оно состоит в том, что одна и та же задача решена различными численными методами. В данном случае выбор метода не влияет на окончательныйрезультат, но бывают ситуации, когда применение того или иного методаимеет решающее значение.

8.4. О численных методахрешения систем уравнений*
Если вы решаете "хорошие" уравнения, как все те, которые были приведеныв предыдущих разделах, то можете никогда не задумываться, как именноMathCAD ищет их корни. Однако даже в этом случае полезно представлять,что происходит "за кадром", т. е. какие действия совершаются в промежуткемежду введением необходимых условий после ключевого слова Given и получением результата после применения функции Find. Это важно хотя бы спозиций выбора начальных значений переменных перед вычислительнымблоком. Рассмотрим в данном разделе некоторые особенности численныхметодов и возможности установки их различных параметров, которые предоставляет MathCAD.
Функция Find реализует градиентные численные методы. Покажем их основную идею на примере уравнения с одним неизвестным f (x)=o для функции f (х)=х²+5х+2, график которой показан на рис. 8.4. Основная идея градиентных методов состоит в последовательных приближениях к истинномурешению уравнения, которые вычисляются с помощью производной отf(x). Приведем наиболее простую форму алгоритма, называемого методомНьютона:
1. За нулевую итерацию принимается введенное пользователем начальноезначение хО=х.
2. В точке хо методом конечных разнос и вычисляется производная f (xO).
3. Пользуясь разложением Тейлора, можно заменить f (х) в окрестности хОкасательной - прямой линией f (x) = f(xO)+f (xO)-(x-xO).
4. Определяется точка xi, в которой прямая пересекает ось х (см. рис. 8.4).
5. Если f (х1)<тоь, то итерации прерываются, и значение xi выдается в качестве решения. В противном случае xi принимается за новую итерацию,и цикл повторяется: строится касательная к f (х) в точке xl, определяетсях2 - точка ее пересечения с осью х и т. д.


Рис. 8.4. Иллюстрацияметода Ньютона
Модификация алгоритма Ньютона для решения системы нескольких уравнений заключается в линеаризации соответствующих функций многих переменных, т. е. аппроксимации их линейной зависимостью с помощьючастных производных. Например, для нулевой итерации в случае системыдвух уравнений используются выражения типа:

Чтобы отыскать точку, соответствующую каждой новой итерации, требуетсяприравнять оба равенства нулю, т. е. решить на каждом шаге полученнуюсистему линейных уравнений.
MathCAD предлагает три различных вида градиентных методов. Чтобы поменять численный метод:
1. Щелкните правой кнопкой мыши на названии функции Find.
2. Наведите указатель мыши^а пункт Nonlinear (Нелинейный) в контекстном меню.
3. В появившемся подменю (рис. 8.5) выберите один из трех методов:Conjugate Gradient (Сопряженных градиентов), Quasi-Newton (Квази-Нью-тоновский) или Levenberg-Marquardt (Левенберга).


Рис. 8.5. Смена численногометода
Чтобы вернуть автоматический выбор типа численного метода, в контекстном меню надо выбрать пункт AutoSelect (Автоматический выбор). Если установлена опция автоматического выбора (о чем говорит флажок, установленный в пункте AutoSelect), то текущий тип численного метода можно узнать, вызвав то же самое подменю и посмотрев, который из них отмеченточкой. Два последних метода являются квази-Ньютоновскими, основнаяидея которых была рассмотрена выше. Первый из них, метод сопряженныхградиентов, является двухшаговым, - для поиска очередной итерации ониспользует как текущую, так и предыдущую итерации. Алгоритм Левенбергаподробно описан в справочной системе MathCAD, а подробную информацию о методах Ньютона и сопряженных градиентов можно найти в большинстве книг по численным методам.
Помимо выбора самого метода, имеется возможность устанавливать их некоторые параметры. Для этого нужно вызвать с помощью того же контекстного меню диалоговое окно Advanced Options (Дополнительные параметры),выбрав в контекстном меню пункты Nonlinear / Advanced options(Нелинейный / Дополнительные параметры). В этом диалоговом окне(рис. 8.6) имеются три группы переключателей, по два в каждой. В первойстроке Derivative estimation (Аппроксимация производной) определяется метод вычисления производной Forward (Вперед) или Central (Центральная).Они соответствуют аппроксимации производной либо правой (двухточечнаясхема "вперед"), либо центральной (трехточечная симметричная схема) конечной разностью.

Примечание
Обратите внимание, что вычисление производной в градиентных численныхметодах решения уравнений производится более экономичным способом, нежели при численном дифференцировании (см. гл. 7).

Во второй строке Variable estimation (Аппроксимация переменных) можноопределить тип аппроксимации рядом Тейлора. Для рассмотренного нами в
этом разделе случая аппроксимации касательной прямой линией выберитепереключатель Tangent (Касательная), для более точной квадратичной аппроксимации (параболой), выберите Quadratic (Квадратичная). Наконец,последняя группа переключателей Linear variable check (Проверка линейности) позволяет в специфических задачах сэкономить время вычислений. Если вы уверены, что нелинейности всех функций, входящих в уравнение, мало сказываются на значениях всех их частных производных, то установитепереключатель Yes (Да). В этом случае производные будут приняты равнымиконстантам и не будут вычисляться на каждом шаге.

Совет
С осторожностью изменяйте параметры численных методов. Пользуйтесь ими,когда решение не находится при выставленных по умолчанию параметрах, иликогда расчеты занимают очень продолжительное время.



Рис. 8.6. Диалоговое окноAdvanced Options
Как мы убедились в этом разделе, все градиентные методы, реализованные вфункции Find, требуют многократного вычисления производных. Если выработаете с достаточно гладкими функциями, то градиентные методы обеспечивают быстрый и надежный поиск корня. Для поиска корня недостаточно гладких функций одной переменной: лучше использовать метод секущих(функцию root). Поэтому правильный выбор численного метода и его параметров может помочь при решении нестандартной задачи.

8.5. Приближенное решение уравнений
Иногда приходится заменять задачу отделения корней системы уравненийзадачей поиска экстремума функции многих переменных. Например, когданевозможно найти решение с помощью функции Find, можно попытатьсяпотребовать вместо точного выполнения уравнений условий минимизировать их невязку. Для этого следует в вычислительном блоке вместо функцииFind использовать функцию Minerr, имеющую тот же самый набор параметров. Она также должна находиться в пределах вычислительного блока:
1. xi:=d ... х_м: =с_м - начальные значения для неизвестных.
2. Given - ключевое слово.
3. Система алгебраических уравнений и неравенств, записанная логическими операторами.
4. Minerr (xi,... ,х_м) - приближенное решение системы относительно переменных xi,... ,х_м, минимизирующее невязку системы уравнений.

Примечание
В функции Minerr реализованы те же самые алгоритмы, что и в функции Find,иным является только условие завершения работы численного метода. Поэтому пользователь может тем же самым образом, с помощью контекстного меню(см. разд. 8.4), выбирать численный алгоритм приближенного решения дляфункции Minerr.

Пример использования функции Minerr показан в листинге 8.9. Как видно,достаточно заменить в вычислительном блоке имя функции на Minerr, чтобы вместо точного (с точностью до TOL) получить приближенное решениеуравнения, заданного после ключевого слова Given.
Листинг 8.9. Приближенное решение уравнения,имеющего корень (х=о,у=0)

Листинг 8.9 демонстрирует приближенное решение уравнения k-x²+y²=o, которое при любом значении коэффициента k имеет единственный точныйкорень (х=о,у=0). Тем не менее при попытке решить его функцией Find длябольших k, порядка принятых в листинге, происходит генерация ошибки"No solution was found" (Решение не найдено). Это связано с иным поведением функции f (x,y)=k-x²+y² вблизи ее корня, по сравнению с функциями,приводимыми в качестве примеров выше в этой главе (см. рис. 8.1, 8.2).В отличие от них f (х,у) не пересекает плоскость f (х,у)=о, а лишь касаетсяее (рис. 8.7) в точке (х=о,у=0). Поэтому и найти корень изложенными впредыдущем разделе градиентными методами сложнее, поскольку вблизикорня производные f (х,у) близки к нулю, и итерации могут уводить предполагаемое решение далеко от корня.
Ситуация еще более ухудшается, если наряду с корнем типа касания (см.рис. 8.7) имеются (возможно, весьма удаленные) корни типа пересечения.
Тогда попытка решить уравнение или систему уравнений с помощью функции Find может приводить к нахождению корня второго типа, даже еслиначальное приближение было взято очень близко к первому. Поэтому есливы предполагаете, что система уравнений имеет корень типа касания, намного предпочтительнее использовать функцию Minerr, тем более, что всегда есть возможность проверить правильность решения уравнений простойподстановкой в них полученного решения (см. листинг 8.6).


Рис. 8.7. График функции k-x²+y²
В листинге 8.9 мы рассмотрели пример нахождения существующего решения уравнения. Приведем в заключение пример нахождения функциейMinerr приближенного решения несовместной системы уравнений и неравенств (листинг 8.10). Решение, выдаваемое функцией Minerr, минимизирует невязку данной системы.

Примечание
Согласно своему математическому смыслу, функция Minerr может применяться для построения регрессии серии данных по закону, заданному пользователем (см. гл. 14).

Листинг 8.10. Приближенное решение несовместной системы уравненийи неравенств

Как видно из листинга, в качестве результата выдаются значения переменных, наилучшим образом удовлетворяющие уравнению и неравенствам ------------------------------------------------------- внутри вычислительного блока. Внимательный читатель может обнаружить,что решение, выдаваемое функцией Minerr в рассматриваемом примере, неявляется единственным, поскольку множество пар значений (х,у) в равнойстепени минимизирует невязку данной системы уравнений и неравенств, jПоэтому для различных начальных значений будут получаться разные решения, подобно тому, как разные решения выдаются функцией Find в слу- iчае бесконечного множества корней (см. обсуждение листинга 8.6 в разд. 8.3).Еще более опасен случай, когда имеются всего несколько локальных минимумов функции невязки. Тогда неудачно выбранное начальное приближениеприведет к выдаче именно этого локального минимума, несмотря на то, чтодругой (глобальный) минимум невязки может удовлетворять системе гораздолучше.

8.6.1. Экстремум функции одной переменной
Поиск экстремума функции включает в себя задачи нахождения локального иглобального экстремума. Последние называют еще задачами оптимизации.Рассмотрим конкретный пример функции f(x), показанной графиком нарис. 8.8 на интервале (-2,5). Она имеет глобальный максимум на левой границе интервала, глобальный минимум, локальный максимум, локальныйминимум и локальный максимум на правой границе интервала (в порядкеслева направо).
В MathCAD с помощью встроенных функций решается только задача поискалокального экстремума. Чтобы найти глобальный максимум (или минимум),требуется либо сначала вычислить все их локальные значения и потом выбрать из них наибольший (наименьший), либо предварительно просканировать с некоторым шагом рассматриваемую область, чтобы выделить из нееподобласть наибольших (наименьших) значений функции и осуществить поиск глобального экстремума, уже находясь в его окрестности. Последнийпуть таит в себе некоторую опасность уйти в зону другого локального экстремума, но часто может быть предпочтительнее из соображений экономиивремени.


Рис. 8.8. График функции f (x)=x⁴+5-x³-10-x
Для поиска локальных экстремумов имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно.
- Minimize (f, xi, ... ,х_м) - вектор значений аргументов, при которых функция f достигает минимума;
- Maximize (f, xi,... ,х_м) - вектор значений аргументов, при которых функция f достигает максимума;
 f (xi,... ,х_м,...) - функция;
 xi, ...,х_м- аргументы, по которым производится минимизация(максимизация).
Всем аргументам функции f предварительно следует присвоить некоторыезначения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения. Примерывычисления экстремума функции одной переменной (рис. 8.8) без дополнительных условий показаны в листингах 8.11-8.12. Поскольку никаких дополнительных условий в них не вводится, поиск экстремумов выполняетсядля любых значений х от -°° до °°.
Листинг 8.11. Минимум функции одной переменной

Листинг 8.12. Максимум функции одной переменной

Kак видно из листингов, существенное влияние на результат оказывает выбор начального приближения, в зависимости от чего в качестве ответа выдаются различные локальные экстремумы. В последнем случае численныйметод вообще не справляется с задачей, поскольку начальное приближениех=-ю выбрано далеко от области локального максимума, и поиск решенияуходит в сторону увеличения f (х), т. е. расходится к х->».

8.6.2. Условный экстремум
В задачах на условный экстремум функции минимизации и максимизациидолжны быть включены в вычислительный блок, т. е. им должно предшествовать ключевое слово Given. В промежутке между Given и функцией поиска экстремума с помощью булевых операторов записываются логическиевыражения (неравенства, уравнения), задающие ограничения на значенияаргументов минимизируемой функции. В листинге 8.13 показаны примерыпоиска условного экстремума на различных интервалах, определенных неравенствами. Сравните результаты работы этого листинга с двумя предыдущими.
Листинг 8.13. Три примера поиска условного экстремума функции

Не забывайте о важности выбора правильного начального приближения и вслучае задач на условный экстремум. Например, если вместо условия -з<х<ов последнем примере листинга задать -5<х<о, то при том же самом начальном х=-ю будет найден максимум Maximize(f,x)=-o.944, что неверно, поскольку максимальное значение достигается функцией f (х) на левой границе интервала при х=-5. Выбор начального приближения х=-4 решает задачуправильно, выдавая в качестве результата Maximize (f,x) =-5.

8.6.3. Экстремум функции многих переменных
Вычисление экстремума функции многих переменных не несет принципиальных особенностей по сравнению с функциями одной переменной. Поэтому ограничимся примером (листинг 8.14) нахождения максимума и минимума функции, показанной в виде графиков трехмерной поверхности илиний уровня на рис. 8.9. Привлечем внимание читателя только к тому, какс помощью неравенств, введенных логическими операторами, задается область на плоскости (X,Y).


Рис. 8.9. График функции f (х,у)и отрезок прямой х+у=10
Листинг 8.14. Экстремум функции двух переменных

Дополнительные условия могут быть заданы и равенствами. Например, определение после ключевого слова Given уравнения х+у=ю приводит к такомурешению задачи на условный экстремум:
Как нетрудно сообразить, еще одно дополнительное условие привело к тому, что численный метод ищет минимальное значение функции f(x,y)вдоль отрезка прямой, показанного на рис. 8.9.

Примечание
Поиск минимума можно организовать и с помощью функции Minerr. Для этогов листинге 8.14 надо поменять имя функции Minimize на Minerr, а после ключевого слова Given добавить выражение, приравнивающее функции f (х,у)значение, заведомо меньшее минимального, например f (x, у) = 0.

8.6.4. Линейное программирование*
Задачи поиска условного экстремума функции многих переменных частовстречаются в экономических расчетах для минимизации издержек, финансовых рисков, максимизации прибыли и т. п. Целый класс экономическихзадач оптимизации описывается системами линейных уравнений и неравенств. Они называются задачами линейного программирования. Приведемхарактерный пример т. н. транспортной задачи, которая решает одну изпроблем оптимальной организации доставки товара потребителям с точкизрения экономии транспортных средств (листинг 8.15).
Листинг 8.15. Решение задачи линейного программирования

Модель типичной транспортной задачи следующая. Пусть имеется N предприятий-производителей, выпустивших продукцию в количестве Ь₀, ...,b_N-iтонн. Эту продукцию требуется доставить м потребителям в количествеао,..., а_м-1 тонн каждому. Численное определение векторов а и ь находитсяв первой строке листинга. Сумма всех заказов потребителей а± равна суммепроизведенной продукции, т. е. всех bi (проверка равенства во второй строке). Если известна стоимость перевозки тонны продукции от 1-го производителя к j-му потребителю с_ч, то решение задачи задает оптимальное распределение соответствующего товаропотока х_ц с точки зрения минимизациисуммы транспортных расходов. Матрица с и минимизируемая функция f (х)матричного аргумента х находятся в середине листинга 8.15.
Условия, выражающие неотрицательность товаропотока, и равенства, задающие сумму произведенной каждым предприятием продукции и суммузаказов каждого потребителя, находятся после ключевого слова Given. Решение, присвоенное матричной переменной sol, выведено в последнейстроке листинга вместе с соответствующей суммой затрат. Обратите внимание, что для получения результата пришлось увеличить погрешность CTOL,задающую максимальную допустимую невязку дополнительных условий.В строке, предшествующей ключевому слову Given, определяются нулевыеначальные значения для х простым созданием нулевого элемента матрицы
Если взять другие начальные значения для х, решение, скорее всего, будетдругим! Возможно, вы сумеете отыскать другой локальный минимум, которыйеще больше минимизирует транспортные затраты. Это еще раз доказывает,что задачи на глобальный минимум, к классу которых относится линейное программирование, требуют аккуратного отношения в смысле выбора начальных значений. Часто ничего другого не остается, кроме сканирования всей областиначальных значений, чтобы из множества локальных минимумов выбрать наиболее глубокий.

8.7. Символьное решение уравнений
Некоторые уравнения можно решить точно с помощью символьного процессора MathCAD. Делается это очень похоже на численное решение уравнений с применением вычислительного блока. Присваивать неизвестнымначальные значения нет необходимости. Листинги 8.16 и 8.17 демонстрируют символьное разрешение уравнения с одним неизвестным и системы двухуравнений соответственно.
Листинг 8.16. Символьное решение алгебраического уравненияс одним неизвестным

Листинг 8.17. Символьное решение системы алгебраических уравнений

Как видно, вместо знака равенства после функции Find в листингах следуетзнак символьных вычислений, который можно ввести с панели Symbolic(Символика) или, нажав клавиши <Ctrl>+<.>. He забывайте, что сами уравнения должны иметь вид логических выражений, т. е. знаки равенства нуж но вводить с помощью панели Booleans (Булевы операторы). Обратите внимание, что в листинге 8.17 вычислены как два первых действительных корня, которые мы уже находили численным методом (см. разд. 8.3).С помощью символьного процессора решить уравнение с одним неизвестным можно и по-другому:
1. Введите уравнение, пользуясь панелью Booleans (Булевы операторы) илинажав клавиши <Ctrl>+<> для получения логического знака равенства,например, х²+2-х-4=о.
2. Щелчком мыши выберите переменную, относительно которой вы собираетесь решить уравнение.
3. Выберите в меню Symbolics (Символика) пункт Variable / Solve(Переменная / Решить).
После строки с уравнением появится строка с решением или сообщение оневозможности символьного решения этого уравнения.
В данном примере после осуществления описанных действий появляетсявектор, состоящий из двух корней уравнения
Символьные вычисления могут производиться и над уравнениями, в которые, помимо неизвестных, входят различные параметры. В листинге 8.18приведен пример решения уравнения четвертой степени с параметром а.Как видите, результат получен в аналитической форме.
Листинг 8.18. Символьное решение уравнения, зависящего от параметра

В следующем разделе мы рассмотрим более подробно, как с помощьюMathCAD можно численными методами решать подобные задачи.

8.8. Метод продолжения по параметру*
Решение "хороших" нелинейных уравнений и систем типа тех, которые были рассмотрены в предыдущих разделах этой главы, представляет собой несложную, с вычислительной точки зрения, задачу. В реальных инженерных и научных расчетах очень распространена более сложная проблема: решениене одного уравнения (или системы), а целой серии уравнений, зависящих отнекоторого параметра (или нескольких параметров). Для таких задач существуют очень эффективные методы, которые называются методами продолжения. Эти методы непосредственно не встроены в MathCAD, но могутбыть легко запрограммированы с помощью уже рассмотренных намисредств. Будем далее говорить об одном уравнении, имея в виду, что всегдавозможно обобщение результатов на случай системы уравнений.
Пусть имеется уравнение f (а,х)=о, зависящее не только от неизвестного х,но и от параметра а. Требуется определить зависимость его корня х от параметра а, т. е. х(а). Простой пример такой задачи был приведен в предыдущем разделе в листинге 8.18. Тогда нам повезло, и решение в общем видебыло найдено с помощью символьных вычислений. Рассмотрим еще один,чуть более сложный пример, аналитическое решение которого также заранееизвестно, но с которым символьный процессор, тем не менее, не справляется. Обобщим задачу (1 - 1), добавив зависимость от параметра а следующимобразом: sin(a'X)=0. (1)


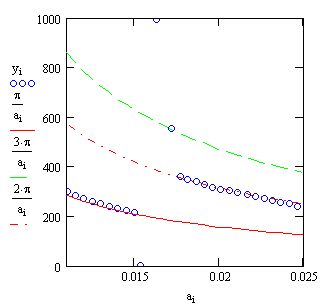
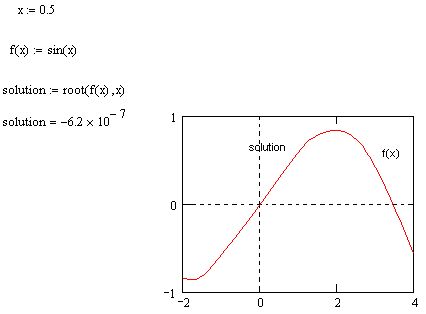
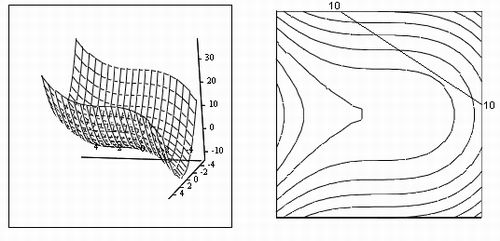
Рис. 8.10. Решение уравнения sin (а-х) =0 (см. листинг 8.21)
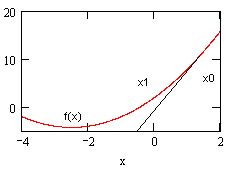
Аналитическое решение этого уравнения находится из соотношения,т. е. имеется бесконечное количество (для каждого N) семейств решений x_N=N-n/a. Несколько из семейств для N=1,2,3 показаны нарис. 8.10 тремя сплошными кривыми. Кроме того, следует иметь в виду, чтодля N=O, т. е. х=о, решением является прямая, совпадающая с осью х. Заме тим (листинг 8.19), что символьный процессор MathCAD выдает в качестверешения только эту серию х=о.
Листинг 8.19. Символьное решение уравнения sin(a-x)=0


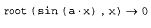
Забудем на время, что аналитическое решение известно, и подойдем к уравнению (1) как к любой другой новой задаче. Решим его методом секущих,применяя для этого встроенную функцию root. Самый простой, но далеконе лучший способ иллюстрируется листингом 8.20. Корень уравнения (1)требуется определить численно для каждого значения параметра а. Дляэтого первые две строки листинга создают ранжированную переменную i,с помощью которой определяется вектор значений параметра а_ь для которых будут производиться расчеты. Его элементы пробегают значения ото.ою до 0.025 с шагом o.ooo5 (эти числа взяты ради примера, вы можетепоэкспериментировать с другими значениями). Последняя строка листингаприсваивает элементам еще одного вектора у вычисленные с помощьюфункции root значения корней уравнения (1) для каждого а±. Но для тогочтобы функция root заработала, необходимо предварительно задать начальное приближение к решению, что сделано в третьей строке листинга. Ключевой момент метода, примененного в листинге 8.20, заключается в том, чтоодно и то же начальное значение х=зоо использовано для всех ai.
Листинг 8.20. Один из способов численного решенияуравнения sin (а-х) =0


Результат расчетов yi показан на том же рис. 8.10 точками, причем самаялевая точка отвечает начальному значению у₀=зоо. Обратите внимание, что,по мере увеличения а, кривая корней уравнения сначала идет по семействурешений у=я/а, а потом (в районе а=ол?) "перепрыгивает" на другое семейство у=2-я/а. С вычислительной точки зрения такая ситуация чаще всегокрайне неблагоприятна, поскольку хотелось бы отыскать непрерывное семейство решений. Скачки зависимости у (а) могут вводить пользователя взаблуждение, вовсе скрывая от него существование семейства решений при а>0.17.
Почему же происходят эти скачки с одного семейства решений на другое?Конечно, причина кроется в выборе начального значения для вычисления каждого из корней. Линия начальных значений у=зоо обозначена на рис. 8.7в виде пунктирной горизонтальной прямой. Для a₀=o.oi, и вообще для нескольких первых ai начальное значение у=зоо находится ближе всего к нижнему семейству решений у=л/а. Поэтому неудивительно, что численный метод находит именно эти корни. В правой части графика на рис. 8.10 к линииначальных значений ближе второе семейство решений у=2-я/а, к ним-то иприводит численный метод.
Приведенные соображения диктуют очень простой рецепт избавления отскачков и нахождения одного из семейств непрерывных решений. Для этоготребуется при поиске каждого (i+i)-ro корня взять начальное значение, повозможности близкое к отыскиваемому семейству. Неплохим вариантом будет выбор приближения в виде предыдущего 1-го корня, который был найден для прошлого значения параметра ai. Возможный вариант воплощенияэтого метода, называемого продолжением по параметру, приведен на листинге 8.21. В нем функция root применена внутри функции пользователяf(xd,a), определенной в самом начале листинга с помощью средств программирования. Назначение функции f (xO,a) заключается в том, что онавыдает значение корня для заданного значения параметра а и начальногоприближения к решению хО. В остальном, смысл листинга 8.21 повторяетпредыдущий, за исключением того, что задается явно (в его предпоследнейстроке) только начальное значение у₀=зоо только для поиска у^. Для всехпоследующих точек, как следует из последней строки листинга, взято начальное значение, равное предыдущему корню yi.
Листинг 8.21. Решение уравнения sin (а-х) =0 методом продолжения к параметру


Результат вычислений, приведенный на рис. 8.11, разительно отличается отпредыдущего. Как видно, столь малое изменение идеологии применениячисленного метода привело к определению непрерывного семейства корней.Отметим, что получить результат рис. 8.10 (без продолжения по параметру)в терминах введенной нами функции f (xO,a) можно, изменив ее первыйаргумент в последней строке листинга 8.21 на константу: f (300,ai).
Чтобы найти другое семейство решений, нужно взять соответствующее первое начальное значение у₀, например, у₀=бОО. Результат действия листинга 8.21 для этого случая показан на рис. 8.12. Если взять у₀ ближе к третьемусемейству решений (например, у₀=эоо), то оно и будет найдено вычислительным процессором MathCAD, и т. д.


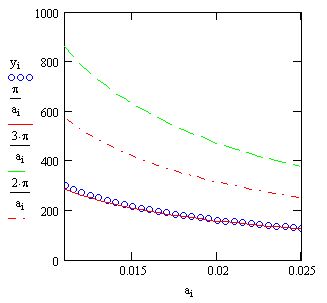
Рис. 8.11. Решение уравнения sin(a-x)=0 методом продолжениядля уо=300 (листинг 8.21)


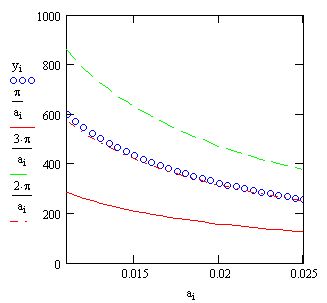
Рис. 8.12. Решение уравнения sin(a-x)=0 методом продолженияпо параметру для у₀=600
С помощью метода продолжения можно решать и соответствующие задачиоптимизации, зависящие от параметра. Идеология в этом случае остаетсяточно такой же, но вместо функций решения нелинейных уравнений rootили Find вам следует применить одну из функций поиска экстремума Minerr, Maximize ИЛИ Minimize.
Мы привели основную идею и один из возможных способов реализацииметода продолжения по параметру. Безусловно, вы можете предложить иныекак математические, так и программистские решения этой проблемы. В частности, для выбора очередного начального приближения к корню можноиспользовать результат экстраполяции уже найденной зависимости х(а),придумать более сложные алгоритмы для ветвящихся семейств решенийи т. д.

Глава 7 Содержание Глава 9