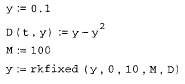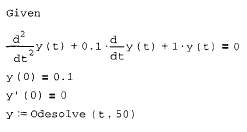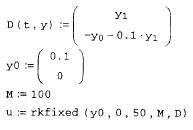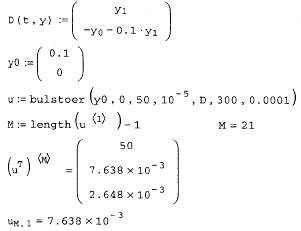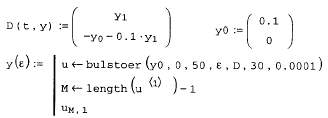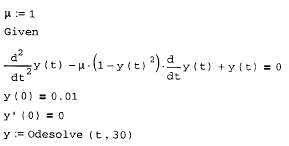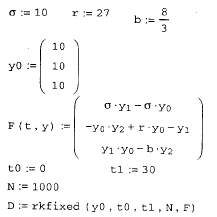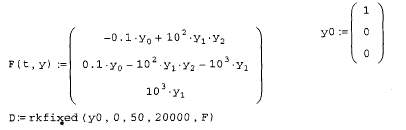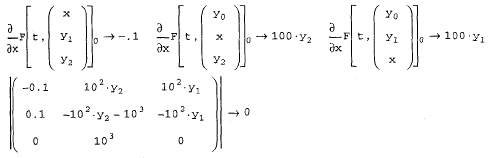• 11.1. ОДУ первого порядка
  • 11.1.1. Вычислительный блок Given/Odesolve
  • 11.1.2. Встроенные функции rkfvxed, Rkadapt, Bulstoer
• 11.2. ОДУ высшего порядка
• 11.3. Системы ОДУ первого порядка
  • 11.3.1. Встроенные функции для решения систем ОДУ
  • 11.3.2. Решение систем ОДУ в одной заданной точке
  • 11.3.3. Некоторые примеры*
• 11.4. Фазовый портрет динамической системы*
• 11.5. Жесткие системы ОДУ
  • 11.5.1. Что такое жесткие ОДУ?
  • 11.5.2. Функции для решения жестких ОДУ

11.1.1. Вычислительный блок Given/Odesolve
Вычислительный блок для решения одного ОДУ, реализующий численныйметод Рунге-Кутты, состоит из трех частей:
Given - ключевое слово;
ОДУ и начальное условие, записанное с помощью логических операторов, причем начальное условие должно быть в форме y(tO)=b;
odesoive(t,tl) - встроенная функция для решения ОДУ относительнопеременной t на интервале (to,ti).

Примечание
Допустимо, и даже часто предпочтительнее, задание функцииOdesolve (t, tl, step) с тремя параметрами, где step- внутренний параметрчисленного метода, определяющий количество шагов, в которых метод Рунге-Кутты, будет рассчитывать решение дифференциального уравнения. Чембольше step, тем с лучшей точностью будет получен результат, но тем большевремени будет затрачено на его поиск. Помните, что подбором этого параметраможно заметно (в несколько раз) ускорить расчеты без существенного ухудшения их точности.

Пример решения задачи Коши для ОДУ первого порядка у'=у-у² посредством вычислительного блока приведен в листинге 11.1.
Листинг 11.1. Решение задачи Коши для ОДУ первого порядка

Не забывайте о том, что вставлять логические операторы следует при помощи панели инструментов Boolean (Булевы операторы). При вводе с клавиатуры помните, что логическому знаку равенства соответствует сочетаниеклавиш <Ctrl>+<=>. Символ производной можно ввести как средствамипанели Calculus (Вычисления), как это сделано в листинге 11.1, так и в видештриха, набрав его с помощью сочетания клавиш <Ctrl>+<F7>(соответствующий пример будет приведен ниже в листинге 11.3.) Выбирайтетот или иной способ представления производной из соображений наглядности представления результатов - на ход расчетов он не влияет.
MathCAD требует, чтобы конечная точка интегрирования ОДУ лежала правее начальной: to<ti (в листинге 11.1 to=o,ti=io), иначе будет выдано сообщение об ошибке. Как можно заметить, результатом применения блокаGiven/odesoive является функция y(t), определенная на промежутке(to,ti). Следует воспользоваться обычными средствами MathCAD, чтобыпостроить ее график или получить значение функции в какой-либо точкеуказанного интервала, например: у(3) =0.691.
Пользователь имеет возможность выбирать между двумя модификациямичисленного метода Рунге-Кутты. Для смены метода необходимо нажатиемправой кнопки мыши на области функции odesoive вызвать контекстноеменю и выбрать в нем один из двух пунктов: Fixed (Фиксированный шаг)или Adaptive (Адаптивный). По умолчанию применяется первый из них, т. е.метод Рунге-Кутты с фиксированным шагом. Подробнее о различии этих методов сказано в разд. 11.3.

11.1.2. Встроенные функцииrkfixed, Rkadapt, Bulstoer
Альтернативный метод решения ОДУ перешел из прежних версий MathCAD.Он заключается в использовании одной из встроенных функций rkfixed,Rkadapt или Bulstoer. Этот способ несколько проигрывает первому и в про стоте, и в наглядности. Поэтому я советую предпочесть вычислительный Iблок Given/odesoive. Однако иногда приходится решать ОДУ первого порядка с помощью второго способа, например, при следующих обстоятельствах:
- вы работаете одновременно с более старыми версиями MathCAD 5.0-8.0или менее мощной разновидностью MathCAD 2001 Standard и хотите,чтобы ваши документы воспринимались каждой из них корректно;
- одно ОДУ решается в контексте решения более сложных задач, в которые входят системы дифференциальных уравнений (для которых вычислительный блок неприменим) - в этом случае может потребоваться единый стиль программирования;
- ответ предпочтительнее получить в виде вектора, а не функции;
- вы привыкли к записи ОДУ в старых версиях MathCAD, у вас много документов, созданных с их помощью и т. п.
Поскольку решение вторым способом одного ОДУ мало чем отличается отрешения систем ОДУ (см. разд. 11.3), приведем пример его использованияв задаче из листинга 11.1 практически без комментариев (см. листинг 11.2) ис помощью одной из трех существующих для этих целей встроенных функций rkfixed. Обратите внимание только на необходимость явного заданияколичества точек интегрирования ОДУ м=юо в третьей строке листинга,а также на получение результата, в отличие от вычислительного блока, не ввиде функции, а в виде матрицы размерности мх2. Она состоит из двухстолбцов: в одном находятся значения аргумента t (от to до ti включительно), а в другом соответствующие значения искомой функции y(t).
Листинг 11.2. Решение задачи Коши для ОДУ первого порядкавторым способом


Совет
В листинге 11.2 приведен пример не лучшего стиля MathCAD-программиро-вания. Сначала переменной у присвоено значение скаляра у=0.1, а затем этойже переменной присвоено матричное значение (результат решения ОДУ). Старайтесь избегать такого стиля, который ухудшает читаемость программы и может приводить, в более сложных случаях, к трудно опознаваемым ошибкам.Неплохим решением было бы назвать результат по-другому, например и.

График решения рассматриваемого уравнения показан на рис. 11.1. Обратите внимание, что он соответствует получению решения в матричном виде (листинг 11.2), поэтому по осям отложены соответствующие столбцы, выделенные из матрицы у оператором <>.

Примечание
Пример, решенный в листингах 11.1-11.2, взят из области математическойэкологии и описывает динамику популяций с внутривидовой конкуренцией.Сначала происходит рост численности популяции, близкий к экспоненциальному, а затем выход на стационарное состояние.



Рис. 11.1. Решение уравнения у'=у-у²(листинг 11.2)

11.2. ОДУ высшего порядка
Обыкновенное дифференциальное уравнение с неизвестной функцией y(t),в которое входят производные этой функции вплоть до y^(N) (t), называетсяОДУ N-ГО порядка. Если имеется такое уравнение, то для корректной постановки задачи Коши требуется задать N начальных условий на саму функциюy(t) и ее производные от первого до (N-l)-ro порядка включительно.В MathCAD 2001 можно решать ОДУ высших порядков как с помощью вычислительного блока Given/odesoive, так и путем сведения их к системамуравнений первого порядка.
Внутри вычислительного блока:
- ОДУ должно быть линейно относительно старшей производной, т. е.фактически должно быть поставлено в стандартной форме;
- начальные условия должны иметь форму y(t)=b или у (t)=b, а не болеесложную (как например, встречающаяся в некоторых математическихприложениях форма y(t)+y' (t)=b).
В остальном, решение ОДУ высших порядков ничем не отличается от решения уравнений первого порядка (см. разд. П. 1), что иллюстрируется лис тингом 11.3. Как вы помните, допустимо написание производной как в видезнака дифференциала (так в листинге 11.3 введено само уравнение), так ис помощью штриха (так введено начальное условие для первой производной). Не забывайте пользоваться булевыми операторами при вводе уравнений и начальных условий. Полученное решение y(t) показано на рис. 11.2.
Листинг 11.3. Решение задачи Коши для ОДУ второго порядка



Рис. 11.2. Решение уравнения осциллятора(листинг 11.3)

Примечание
В листинге 11.3 решено уравнение затухающего гармонического осциллятора,которое описывает, например, колебания маятника. Для модели маятника y(t)описывает изменения угла его отклонения от вертикали, у¹ (t) - угловую скорость маятника, у'' (t) - ускорение, а начальные условия, соответственно,начальное отклонение маятника у (0) =0.1 и начальную скорость у' (0) = 0.

Второй способ решения ОДУ высшего порядка связан со сведением его кэквивалентной системе ОДУ первого порядка. Покажем на том же примереиз листинга 11.3, как это делается. Действительно, если формально обозна чить y₀(t)sy(t), a yi(t)=y* (t)=yo' (t), то исходное уравнение запишется через функции уо (t) и YI (t)в виде системы двух ОДУ:
Именно эта система решается в качестве примера в разд. 11.3. Таким образом, любое ОДУ N-ГО порядка, линейное относительно высшей производной, можно свести к эквивалентной системе N дифференциальных уравнений.

11.3.1. Встроенные функции для решения систем ОДУ
В Math CAD 2001 имеются три встроенные функции, которые позволяютрешать поставленную в форме (2-3) задачу Коши различными численнымиметодами.
- rkfixed(yO,tO,ti,M,D) - метод Рунге-Кутты с фиксированным шагом;- Rkadapt(yO,to,ti,M,D) - метод Рунге-Кутты с переменным шагом;- Buistoer (yO,to,ti,M,D) - метод Булирша-Штера;
 уо - вектор начальных значений в точке to размера NXI;
 to - начальная точка расчета;
 ti - конечная точка расчета;
 м - число шагов, на которых численный метод находит решение;
 о - векторная функция размера NXI двух аргументов - скалярного t ивекторного у. При этом у - искомая векторная функция аргумента tтого же размера NXI.
Соблюдайте регистр первой буквы рассматриваемых функций, поскольку этовлияет на выбор алгоритма счета, в отличие от многих других встроенныхфункций MathCAD, например Find^f ind (см. разд. 11.3.2).
Каждая из приведенных функций выдает решение в виде матрицы размера(M+i)x(N+i). В ее левом столбце находятся значения аргумента t, делящиеинтервал на равномерные шаги, а в остальных N столбцах - значения искомых функций уо (t), У! (t),..., y_N-i (t), рассчитанные для этих значений аргумента. Поскольку всего точек (помимо начальной) м, то строк в матрицерешения будет всего м+1.
В подавляющем большинстве случаев достаточно использовать первуюфункцию rkfixed, как это показано в листинге 11.4 на примере решениясистемы ОДУ модели осциллятора с затуханием (см. разд. JJ.2).
Листинг 11.4. Решение системы двух ОДУ

Самая важная - это первая строка листинга, в которой, собственно, определяется система ОДУ. Сравните рассматриваемую систему (разд. 11.2-1),записанную в стандартной форме с формальной ее записью в MathCAD,чтобы не делать впоследствии ошибок. Во-первых, функция о, входящая вчисло параметров встроенных функций для решения ОДУ, должна бытьфункцией обязательно двух аргументов. Во-вторых, второй ее аргумент должен быть вектором того же размера, что и сама функция о. В-третьих, точнотакой же размер должен быть и у вектора начальных значений уо (он определен во второй строке листинга).
Не забывайте, что векторную функцию o(t,y) следует определять черезкомпоненты вектора у с помощью кнопки нижнего индекса (Subscript)с наборной панели Calculator (Калькулятор) или нажатием клавиши <[>.В третьей строке листинга определено число шагов, на которых рассчитывается решение, а его последняя строка присваивает матричной переменной ирезультат действия функции rkfixed. Решение системы ОДУ будет осуществлено на промежутке (0,50).
Как выглядит все решение, показано на рис. 11.3. Размер полученной матрицы будет равен <м+1)х(ы+1), т. е. Ю1хз. Просмотреть все компоненты матрицы и, которые не помещаются на экране, можно с помощью вертикаль ной полосы прокрутки, как нетрудно соооразить, на этом рисунке отмечено выделениемрасчетное значение первого искомого вектораУО на 12-м шаге ui₂,i=o.07. Это соответствует, сматематической точки зрения, найденномузначению у₀(б.0)=о.07. Для вывода элементоврешения в последней точке интервала используйте выражения типа u_M,i=7.523xicr³.


Рис. 11.3. Матрица решений системы уравнений(листинг 11.4)
Обратите внимание на некоторое разночтение в обозначении индексов вектораначальных условий и матрицы решения. В ее первом столбце собраны значения нулевой компоненты искомого вектора, во втором столбце - первой компоненты и т. д.
Чтобы построить график решения, надо отложить соответствующие компоненты матрицы решения по координатным осям: значения аргумента и^<0> - вдоль оси х, а и^<1> и и^<2> - вдоль оси Y (рис. 11.4). Как известно, решенияобыкновенных дифференциальных уравнений часто удобнее изображать нев таком виде, а в фазовом пространстве, по каждой из осей которого откладываются значения каждой из найденных функций. При этом аргумент входит в них лишь параметрически. В рассматриваемом случае двух ОДУ такойграфик - фазовый портрет системы - является кривой на фазовой плоскости и поэтому особенно нагляден. Он изображен на рис. 11.5 (слева), иможно заметить, что для его построения потребовалось лишь поменять метки осей на u^<:L> и и^<2> соответственно.

Примечание
Фазовый портрет типа, изображенного на рис. 11.5, имеет одну стационарнуюточку (аттрактор), на которую "накручивается" решение. В теории динамических систем аттрактор такого типа называется фокусом.


Рис. 11.4. График решения системы ОДУ (11.2-1) (листинг 11.4)


Рис. 11.5. Фазовый портрет решения системы ОДУ при м=100 (слева)и М=200 (справа) (листинг 11.4)
В общем случае, если система состоит из N ОДУ, то фазовое пространствоявляется N-мерным. При ы>з наглядность теряется, и для визуализации фазового портрета приходится строить его различные проекции.
На том же рис. 11.5, справа, показан для сравнения результат расчета фазового портрета с большим числом шагов. Видно, что в этом случае обеспечивается лучшая точность, и, в результате, решение получается более гладким.Конечно, при этом увеличивается и время расчетов.
При решении систем ОДУ многие проблемы могут быть устранены при помощипростой попытки увеличить число шагов численного метода. В частности, сделайтетак при неожиданном возникновении ошибки "Found a number with a magnitude greater than 10*307" (Найдено число, превышающее значение 10 ).Данная ошибка может означать не то, что решение в действительности расходится, а просто недостаток шагов для корректной работы численного алгоритма.
В заключение следует сказать несколько слов об особенностях различныхчисленных методов. Все они основаны на аппроксимации дифференциальных уравнений разностными аналогами. В зависимости от конкретной формы аппроксимации, получаются алгоритмы различной точности и быстродействия. В MathCAD использован наиболее популярный алгоритм Рунге-Кутты четвертого порядка, описанный в большинстве книг по методам вычислений. Он обеспечивает малую погрешность для широкого класса системОДУ за исключением жестких систем. Поэтому в большинстве случаев стоитприменять функцию rkfixed. Если по различным причинам время расчетовстановится критичным или точность неудовлетворительна, стоит попробовать вместо rkfixed другие функции, благо сделать это очень просто, благодаря одинаковому набору параметров. Для этого нужно только поменятьимя функции в программе.
Функция Rkadapt может быть полезна в случае, когда известно, что решениена рассматриваемом интервале меняется слабо, либо существуют участкимедленных и быстрых его изменений. Метод Рунге-Кутты с переменнымшагом разбивает интервал не на равномерные шаги, а более оптимальнымспособом. Там, где решение меняется слабо, шаги выбираются более редкими, а в областях его сильных изменений - частыми. В результате для достижения одинаковой точности требуется меньшее число шагов, чем дляrkfixed. Метод Булирша-Штера Pjiistoer часто оказывается более эффективным для поиска гладких решений.

11.3.2. Решение систем ОДУв одной заданной точке
Зачастую при решении дифференциальных уравнений требуется определитьзначения искомых функций не на всем интервале (to,ti), а только в одной его последней точке. Например, весьма распространены задачи поиска аттракторов динамических систем. Известно, что для широкого класса ОДУодна и та же система при разных (или даже любых, как рассмотренный выше пример осциллятора с затуханием) начальных условиях при t приходит в одну и ту же точку (аттрактор). Поэтому часто нужно определитьименно эту точку.
Такая задача требует меньше ресурсов компьютера, чем решение системыОДУ на всем интервале, поэтому в MathCAD 2001 имеются модификациивстроенных функций Rkadapt и Buistoer. Они имеют несколько другой набор параметров и работают быстрее своих аналогов.
- rkadapt (yO, to, ti,acc,D, k,s) - метод Рунге-Кутты с переменным шагом;- buistoer (yO,to,ti,acc,D,k,s) - метод Булирша-Штера;
 уо - вектор начальных значений в точке to;
 to,ti - начальная и конечная точки расчета;
 асе - погрешность вычисления (чем она меньше, тем с лучшей точностью будет найдено решение; рекомендуется выбирать значенияпогрешности в районе o.ooi);
 о - векторная функция, задающая систему ОДУ;
 k - максимальное число шагов, на которых численный метод будетнаходить решение;
 s - минимально допустимая величина шага.
Как легко заметить, вместо числа шагов на интервале интегрирования ОДУ,в этих функциях необходимо задать точность расчета численным методомзначения функций в последней точке. В этом смысле параметр асе похож наконстанту TOL, которая влияет на большинство встроенных численных алгоритмов MathCAD. Количество шагов и их расположение определяется численным методом автоматически, чтобы обеспечить эту точность. Два последних параметра нужны для того, чтобы пользователь мог искусственноповлиять на разбиение интервала на шаги. Параметр k служит для того, чтобы шагов не было чрезмерно много, причем нельзя сделать k>1000. Параметр s - для того, чтобы ни один шаг не был слишком малым для появления больших погрешностей при разностной аппроксимации дифференциальных уравнений внутри алгоритма. Эти параметры следует задавать явно,исходя из свойств конкретной системы ОДУ. Как правило, проведя ряд тестовых расчетов, можно подобрать их оптимальный набор для каждого конкретного случая.
Пример использования функции buistoer для того же примера (11.2-1)приведен в листинге 11.5. В его первых двух строках, как обычно, определяется система уравнений и начальные условия; в следующей строке матрице иприсваивается решение, полученное с помощью buistoer. Структура этой матрицы в точности такая же, как и в случае решения системы ОДУ посредством уже рассмотренных нами ранее встроенных функций (см. разд. 11.3.1).Однако в данном случае нам интересна только последняя точка интервала.Поскольку сделанное численным методом количество шагов, т. е. размерматрицы и, заранее неизвестно, то его необходимо предварительно определить. Это сделано в четвертой строке листинга, присваивающей это числопеременной м, в этой же строке оно выведено на экран. В предпоследнейстроке листинга осуществлен вывод решения системы ОДУ на конце интервала, т. е. в точке t=50 в виде вектора. В последней строке для примера ещераз выводится искомое значение первой функции из системы ОДУ(сравните его с соответствующим местом вектора из предыдущей строки).
Листинг 11.5. Решение системы двух ОДУ

Чтобы попробовать альтернативный численный метод, достаточно в листинге 11.5 заменить имя функции bulstoer На rkadapt.
Функции bulstoer и rkadapt (те, что пишутся с маленькой буквы) не предназначены для нахождения решения в промежуточных точках интервала, хотяони и выдают их в матрице-результате. На рис. 11.6 показаны фазовые портреты рассматриваемой системы ОДУ, полученные с помощью bulstoer(результат листинга 11.5) и с помощью rkadapt (при соответствующей заменетретьей строки листинга 11.5). Видно, что несмотря на высокую точность (10~⁵)и верный результат на конце интервала, левый график мало напоминает правильный фазовый портрет (см. рис. 11.5 или правый график на рис. 11.6), начиная быть приемлемым только при предельно допустимом для обсуждаемыхфункций значении асс=10~¹⁶.


Рис. 11.6. Фазовый портрет, полученный bulstoer (слева) и rkadapt (справа) (листинг 11.5)
В заключение остановимся на влиянии выбора параметра асе на расчеты.Для этого воспользуемся простой программой, представленной на листинге 11.6. В ней из матрицы решения все той же задачи Коши взято лишь полученное значение одной из функции на правой границе интервала. Но затоэтот результат оформлен в виде функции пользователя у(е), в качестве аргумента которой выбран параметр асе функции bulstoer.
Листинг 11,6. Использование решения ОДУ для определенияфункции пользователя

Вычисленный вид у(е) показан на рис. 11.7 вместе с аналогичным результатом для функции rkadapt. Как видно, в данном примере численные методыработают несколько по-разному. Метод Рунге-Кутты дает результат темближе к истинному, чем меньше выбирается е=асс. Метод Булирша-Штерадемонстрирует менее естественную зависимость у (е): даже при относительно больших е реальная точность остается хорошей (намного лучше методаРунге-Кутты). Поэтому для экономии времени расчетов (подчеркнем ещераз: для данной конкретной задачи) в функции bulstoer можно выбирать ибольшие асе.


Рис. 11.7. Зависимостьрасчетного значения одногоиз уравнений системы ОДУна конце интервалаот параметра асе(листинг 11.6)
Чтобы обеспечить заданную точность, алгоритмы, реализованные во встроенных функциях, могут изменять как количество шагов, разбивающих интервал (tO,tl), так и их расположение вдоль интервала. Чтобы выяснить, насколько шагов разбивался интервал при расчетах у(е)на рис. 11.7 для каждого е, следует вычислить размер получающейся матрицы. Для этого можно,например, определить подобные функции:


Рис. 11.8. Зависимостьчисла шагов от параметраасе численных методов
Сравнив два результата применения rkadapt для k=30 и k=ioo, обратитевнимание (рис. 11.8), как еще один параметр - максимальное число шагов k,

Примечание
В большинстве примеров, изложенных ниже, для построения фазового портрета рассчитывается несколько решений для разных начальных условий.

Ограничимся в дальнейшем минимальными комментариями и приведемлистинги и графики решений без подробного обсуждения.
Модель "хищник-жертва"
Модель взаимодействия "хищник-жертва" независимо предложили в 1925-1927 гг. Лотка и Вольтерра. Два дифференциальных уравнения (листинг 11.7)моделируют временную динамику численности двух биологических популяций жертвы уо и хищника у_ь Предполагается, что жертвы размножаются спостоянной скоростью с, а их численность убывает вследствие поеданияхищниками. Хищники же размножаются со скоростью, пропорциональнойколичеству пищи (с коэффициентом г), и умирают естественным образом(смертность определяется константой о). В листинге рассчитываются трирешения о, с, р для разных начальных условий.
влияет на вид м(е). Заметим, что такие же изменения параметра k на расчетм(е) посредством функции bulstoer влияют слабо.
Таким образом, проводя тестовые расчеты для различных задач и подбираянаилучший набор параметров, можно существенно сэкономить ресурсыкомпьютера. Конечно, проводить подобный анализ стоит в случаях, когдавремя расчетов играет важную роль.

11.3.3. Некоторые примеры*
В предыдущих разделах были использованы примеры исключительно линейных уравнений, т. е. содержащих только первую степень неизвестных функций и их производных. Между тем, многие нелинейные уравнения демонстрируют совершенно удивительные свойства, причем решение большинстваиз них можно получить лишь численно. Рассмотрим несколько наиболееизвестных классических примеров систем ОДУ, имея в виду, что читателюони могут пригодиться как в познавательных, так и в практических целях.Это модели динамики популяций (Вольтерры), генератора автоколебаний(Ван дер Поля), турбулентной конвекции (Лоренца) и химической реакциис диффузией (Пригожина). Все они (впрочем, как и уже приведенные вышев этой главе) содержат производные по времени t и описывают динамикуразличных физических параметров. Задачи Коши для таких моделей называют динамическими системами, и для их изучения центральным моментомявляется анализ фазовых портретов, т. е. решений, получающихся при выборе всевозможных начальных условий.
Листинг 11,7. Модель "хищник-жертва"

Модель замечательна тем, что в такой системе наблюдаются циклическоеувеличение и уменьшение численности и хищника (рис. 11.9), и жертвы, такчасто наблюдаемое в природе. Фазовый портрет системы представляет собойконцентрические замкнутые кривые, окружающие одну стационарную точку, называемую центром. Как видно, модельные колебания численностиобеих популяций существенно зависят от начальных условий - после каждого периода колебаний система возвращается в ту же точку. Динамическиесистемы с таким поведением называют негрубыми.


Рис. 11.9. График решения (слева) и фазовый портрет (справа) системы "хищник-жертва" (листинг 11.7)
Автоколебания
Рассмотрим решение уравнения Ван дер Поля, описывающего электрические колебания в замкнутом контуре, состоящем из соединенных последо вательно конденсатора, индуктивности, нелинейного сопротивления и элементов, обеспечивающих подкачку энергии извне (листинг 11.8). Неизвестная функция времени y(t) имеет смысл электрического тока, а в параметре ц заложены количественные соотношения между составляющими электрической цепи, в том числе и нелинейной компонентой сопротивления.
Листинг 11.8. Модель Ван дер Поля (р=1)



Рис. 11.10. График решения (слева) и фазовый портрет (справа) уравнения Ван дер Поля (листинг 11.8)
Решением уравнения Ван дер Поля являются колебания, вид которых дляц=1 показан на рис. 11.10. Они называются автоколебаниями и принципиально отличаются от рассмотренных нами ранее (например, колебаний маятника в разд. П.3.2) тем, что их характеристики (амплитуда, частота, спектр)не зависят от начальных условий, а определяются исключительно свойства ми самой динамической системы. Через некоторое время расчетов послевыхода из начальной точки решение выходит на один и тот же цикл колебаний, называемый предельным циклом. Аттрактор типа предельного цикла является замкнутой кривой на фазовой плоскости. К нему асимптотическипритягиваются все окрестные траектории, выходящие из различных начальных точек, как изнутри (рис. 11.10), так и снаружи (рис. 11.11) предельногоцикла.


Рис. 11.11. Решение уравнения Ван дер Поля при других начальных условиях у=-2,у'=-3

Примечание
Если компьютер у вас не самый мощный, то расчет фазового портрета срис. 11.10-11.11 в MathCAD может занять относительно продолжительноевремя, что связано с численным определением сначала решения у (t), а потомего производной. Время расчетов можно было бы существенно сократить, еслииспользовать вместо вычислительного блока Given/Odesolve одну из встроенных функций, которые выдают решение в виде матрицы, например, rkf ixed.

Аттрактор Лоренца
Одна из самых знаменитых динамических систем предложена в 1963 г. Лоренцем в качестве упрощенной модели конвективных турбулентных движений жидкости в нагреваемом сосуде тороидальной формы. Система состоитиз трех ОДУ и имеет три параметра модели (листинг 11.9). Поскольку неизвестных функций три, то фазовый портрет системы должен определяться нена плоскости, а в трехмерном пространстве.
Листинг 11.9. Модель Лоренца

Решением системы Лоренца при определенном сочетании параметров(рис. 11.12) является странный аттрактор (или аттрактор Лоренца) - притягивающее множество траекторий на фазовом пространстве, которое повиду идентично случайному процессу. В некотором смысле, аттрактор Лоренца является стохастическими автоколебаниями, которые поддерживаютсяв динамической системе за счет внешнего источника.


Рис. 11.12. Аттрактор Лоренца (листинг 11.9)
Решение в виде странного аттрактора появляется только при некоторых сочетаниях параметров. В качестве примера на рис. 11.12 приведен результат для г=10 и тех же значений остальных параметров. Как видно, аттрактором вэтом случае является фокус. Перестройка типа фазового портрета происходит в области промежуточных г. Критическое сочетание параметров, прикоторых фазовый портрет системы качественно меняется, называется в теории динамических систем точкой бифуркации. Физический смысл бифуркации в модели Лоренца, согласно современным представлениям, описываетпереход ламинарного движения жидкости к турбулентному.


Рис. 11.13. Решение системы Лоренца с измененным параметром г=10
Замечательно, что решение подобных нелинейных динамических системможно получить только численно, поэтому их изучение стало бурно развиваться с ростом возможностей вычислительной техники в последние полвека.

11.4. Фазовый портретдинамической системы*
До сих пор в этой главе в качестве примеров расчета динамических системмы приводили графики 1-3 траекторий на фазовой плоскости. Однако длянадежного исследования фазового портрета необходимо решить системуОДУ большое количество раз с самыми разными начальными условиями(и, возможно, с разным набором параметров модели), чтобы посмотреть,к каким аттракторам сходятся различные траектории. В MathCAD можнореализовать эту задачу, например, в форме алгоритма, приведенного в листинге 11.10 для решения системы уравнений автокаталитической химиче ской реакции с диффузией. Эта модель, называемая моделью брюсселятора,предложена в 1968 г. Лефевром и Пригожиным. Неизвестные функции отражают динамику концентрации промежуточных продуктов некоторой реальной химической реакции. Параметр модели в равен исходной концентрации катализатора.
Листинг 11.10. Построение фазового портрета для модели брюсселятора

Предложенный алгоритм формирует из отдельных матриц решений системыОДУ с разными начальными условиями объединенную матрицу. Пары начальных условий задаются в первой строке листинга в виде матрицы v раз-мера 2х10. Последнее означает построение десяти траекторий. Для того чтобы поменять количество траекторий, измените соответствующим образомразмер этой матрицы. Затем (рис. 11.14) элементы матрицы и выводятся на график в виде отдельных точек. Отсутствие соединения точек линиями является недостатком алгоритма, но это плата за возможность представить вMathCAD несложным образом сразу большое количество траекторий на фазовой плоскости.


Рис. 11.14. Фазовый портрет брюсселятора при В=0.5 (листинг 11.10)
Как видно из рис. 11.14, все траектории, вышедшие из разных точек, асимптотически стремятся к одному и тому же аттрактору (1,0.5). Из теории динамических систем нам известно, что такой аттрактор называется узлом(с узлом мы уже встречались в примерах разд. 11.1). Конечно, в общем случаепри анализе фазового портрета желательно "прощупать" большее число траекторий, задавая более широкий диапазон начальных условий. Не исключено, что в других областях фазовой плоскости траектории будут сходитьсяк другим аттракторам.
Эволюцию фазового портрета брюсселятора можно наблюдать, проводя расчеты с различным параметром в. При его увеличении узел будет сначалапостепенно смещаться в точку с координатами (1,в), пока не достигнетбифуркационного значения в=2. В этой точке происходит качественная перестройка портрета, выражающаяся в рождении предельного цикла. Придальнейшем увеличении в происходит лишь количественное изменениепараметров этого цикла. Решение, полученное при в=2.5, показано нарис. 11.15.

Примечание
Чтобы найти аттракторы динамической системы, как известно, нужно решитьсистему алгебраических уравнений, получающуюся из системы ОДУ заменой
нулями их левых частей. Эти задачи также удобно решать средствамиMathCAD (см. гл. 8). В частности, исследование зависимости фазового портрета от параметров системы ОДУ и поиск бифуркаций можно проводить методами продолжения (см. разд. "Метод продолжения по параметру" гл. 8).


Рис. 11.15. Фазовый портрет брюсселятора при В=2.5
Читатели, сталкивающиеся с расчетом динамических систем, несомненнооценят возможности MathCAD по построению фазовых портретов и исследованию бифуркаций. Возможно также, что они найдут лучшие программные решения этой задачи, чем алгоритм, предложенный в данном разделеавтором.

11.5.1. Что такое жесткие ОДУ?
Строгого общепринятого математического определения жестких ОДУ нет.В рамках этой книги будем считать, что жесткие системы - это те уравнения, решение которых получить намного проще с помощью определенных неявных методов, чем с помощью явных методов (типа тех, что оыли рассмотрены в предыдущих разделах). Примерно такое определение было предложено в 1950-х годах классиками в этой области Кертиссом и Хиршфельдером. Начнем разговор о жестких ОДУ с примера нежесткого уравнения(листинг 11.11), решение которого показано на рис. 11.16. На том же графике показано решение подобного ОДУ с другим коэффициентом при правойчасти, равным не-10, а-30. Решение обоих уравнений не составило труда, ичисленный метод Рунге-Кутты дал правильный результат.
Листинг 11.11. Решение нежесткого ОДУ



Рис. 11.16. Решение нежестких ОДУ методом Рунге-Кутты(листинг 11.11)
На рис. 11.17 показано решение того же ОДУ с коэффициентом -50. Вас,несомненно, должен насторожить результат, выданный MathCAD. Характерная "разболтка" решения говорит о неустойчивости алгоритма. Первое,что можно сделать, - увеличить количество шагов в методе Рунге-Кутты. Для этого достаточно добавить третий параметр step в функциюodesoive(t,i,step). После нескольких экспериментов можно подобрать такое значение step, которое будет обеспечивать устойчивость решения. Читатель может самостоятельно убедиться, что при step>20 "разболтка" пропадает, и решение становится похожим на графики, показанные на рис. 11.16.


Рис. 11.17. Неверное решение более жесткого ОДУ методом Рунге-Кутты
Таким образом, во-первых, мы выяснили, что одни и те же уравнения сразными параметрами могут быть как жесткими, так и нежесткими. Во-вторых, чем жестче уравнение, тем больше шагов в обычных численных методах требуется для его устойчивого решения. С классическим примеромОДУ из листинга 11.11 все получилось хорошо, т. к. оно было не очень жестким, и небольшое увеличение числа шагов разрешило все проблемы. Длярешения обычными методами более жестких уравнений требуются миллионы, миллиарды и даже большее число шагов.

Примечание
Некоторые ученые замечают, что в последние годы методы Рунге-Кутты сталиуступать свое главенствующее положение среди алгоритмов решения ОДУ методам, способным решать жесткие задачи.

Исторически, интерес к жестким системам возник в середине XX века приизучении уравнений химической кинетики с одновременным присутствиемочень медленно и очень быстро протекающих химических реакций. Тогданеожиданно оказалось, что считавшиеся исключительно надежными методыРунге-Кутты стали давать сбой при расчете этих задач. Рассмотрим классическую модель взаимодействия трех веществ (Робертсон, 1966), которая какнельзя лучше передает смысл понятия жесткости ОДУ.
Пусть вещество "О" медленно превращается в "1": "0"->"1" (со скоростьюo.l), вещество "1" при каталитическом воздействии самого себя превращается очень быстро в вещество "2": "i"+"i"-»"2"+"i" (ю³). И, наконец, подобным образом (но со средней скоростью) реагируют вещества "2" и "1":
"₁"₊..₂"_^"0»+"2" (ю²). Система ОДУ, описывающая динамику концентрацииреагентов, с попыткой решения методом Рунге-Кутты, приведена в листинге 11.12.
Листинг 11.12. Жесткая система ОДУ химической кинетики

Бросается в глаза сильно различающийся порядок коэффициентов при разных слагаемых. Именно степень этого различия чаще всего и определяетжесткость системы ОДУ. В качестве соответствующей характеристики выбирают матрицу Якоби (якобиан) векторной функции F(t,y), т.е. функциональную матрицу, составленную из производных F(t,y) (см. разд. "Частныепроизводные" гл. 7). Чем вырожденнее матрица Якоби, тем жестче системауравнений. В приведенном примере определитель якобиана и вовсе равеннулю при любых значениях у₀, YI и у₂ (листинг 11.13, вторая строка). В первой строке листинга 11.13 приведено напоминание способа вычисленияякобиана средствами MathCAD на примере определения элементов его первой строки.
Листинг 11.13. Якобиан рассматриваемой системы ОДУ химической кинетики

Для примера, приведенного в листинге 11.12, стандартным методом Рунге-Кутты все-таки удается найти решение (оно показано на рис. 11.18). Однакодля этого требуется очень большое число шагов, м=20000, что делает расчетыочень медленными. При меньшем числе шагов численному алгоритму неудается найти решение. В процессе работы алгоритма оно расходится, и
MathCAD вместо результата выдает ошибку о превышении предельно большого числа.
Еще один факт, на который стоит обратить внимание, - это различие в порядке величины получающегося решения. Как видно из рис. 11.18, концентрация первого реагента yi существенно (в тысячи раз) превышает концентрацию остальных. Это свойство также очень характерно для жесткихсистем.

Примечание
В принципе, можно было бы снизить жесткость системы "вручную", применяямасштабирование. Для этого нужно искусственно уменьшить искомую функциюyi, к примеру, в тысячу раз, разделив все слагаемые в системе ОДУ, содержащие yi, на 1000. После масштабирования для решения полученной системыметодом Рунге-Кутты будет достаточно взять всего м=20 шагов.



Рис. 11.18. Решение жесткой системы ОДУ химической кинетики методомРунге-Кутты (листинг 11.12)

11.5.2. Функции для решения жестких ОДУ
Решение жестких систем дифференциальных уравнений можно осуществитьтолько с помощью встроенных функций, аналогичных по действию семейству рассмотренных выше функций для обычных ОДУ. Отличием является добавление к стандартному набору параметров дополнительной матричнойфункции, задающей якобиан системы ОДУ. Решение выдается в виде матрицы, по форме идентичной аналогичным функциям решения нежесткихзадач Коши.
- stiffb(yO,to,ti,M, F, j) - метод Булирша-Штера для жестких системОДУ;
- stiffr (yO,to,ti,M,F, j) - метод Розенброка для жестких систем ОДУ;
 уО - вектор начальных значений в точке to;
 to,ti - начальная и конечная точки расчета;
 м - число шагов численного метода;
 F - векторная функция F(t,y) размера IXN, задающая систему ОДУ;
 J - матричная функция J(t,y) размера (N+IJXN, составленная из вектора производных функции F(t,y) no t (правый столбец) и ее якобиана (N левых столбцов).
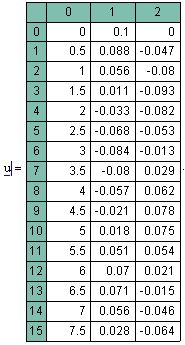
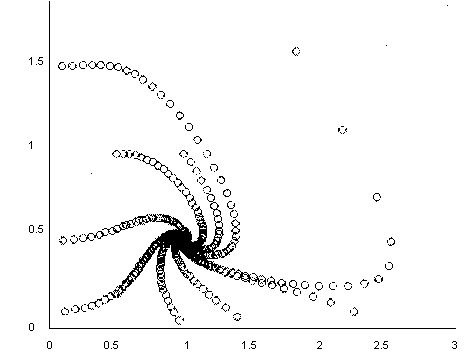
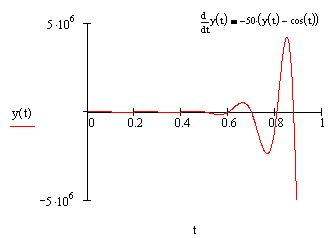
Покажем действие этих алгоритмов на том же примере жесткой системыОДУ химической кинетики (листинг 11.14). Обратите внимание, как следуетпредставлять в данном случае якобиан, сравнив задание матричной функциив предпоследней строке листинга 11.14 с заданием якобиана из листинга 11.13.
Листинг 11.14. Решение жесткой системы ОДУ химической кинетики

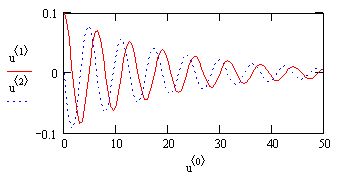
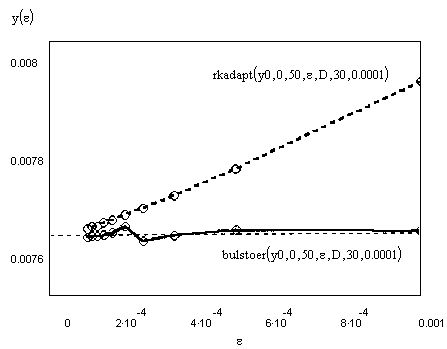
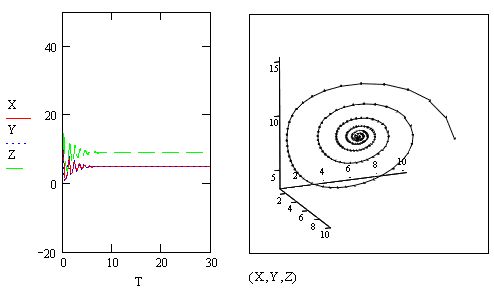
Расчеты показывают, что для получения того же результата (см. рис. 11.18)оказалось достаточно в тысячу раз меньшего количества шагов численного алгоритма, чем для стандартного метода Рунге-Кутты! Примерно во столькоже раз требуется меньше компьютерного времени на проведение расчетов.Стоит ли говорить, что, если вы имеете дело с жёсткими (в той или инойстепени) системами, применение описанных специальных алгоритмов просто необходимо.
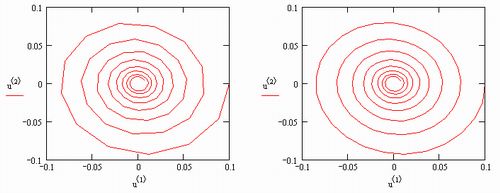
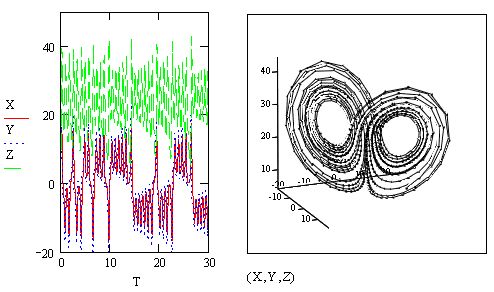
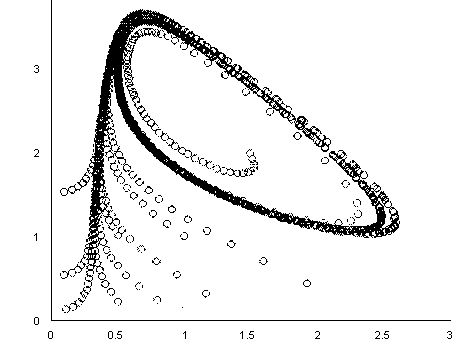
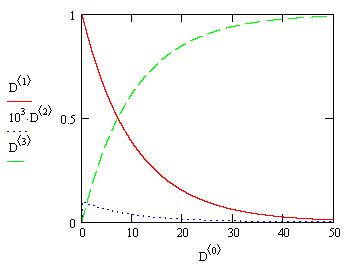
Важно заметить, что до сих пор мы имели дело с примером не очень жесткой системы. Попробуйте вместо скоростей упомянутых химических реакций (см. разд. 11.5.1), 0.1, 10³ и 10² взять другие числа, например о.05, 10⁴ и 10⁷ соответственно. Заметим, что такое соотношение скоростей часто встречается в прикладных задачах химической кинетики и определяет куда болеежесткую систему ОДУ. Ее уже никак не удается решить стандартными методами, поскольку число шагов численного метода должно быть просто гигантским. А между тем, алгоритмы для жестких ОДУ справляются с этойзадачей с легкостью (рис. 11.19), причем практически при тех же значенияхшага, что были взяты в листинге 11.14.


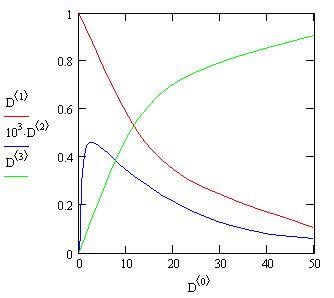
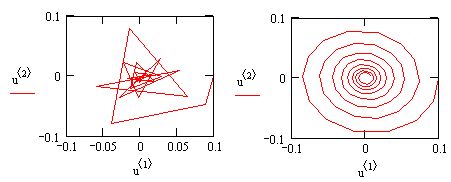
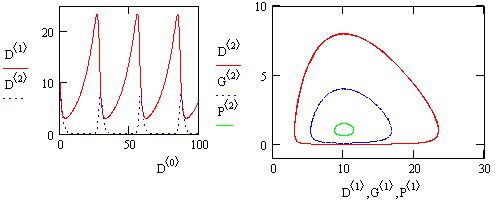
Рис. 11.19. Решение более жесткой системы ОДУ химической кинетики методом Розенброка
Обратите внимание, что порядки величины решений для концентраций различных веществ на рис. 11.19 различаются еще сильнее, чем в предыдущем(менее жестком) примере.

Примечание
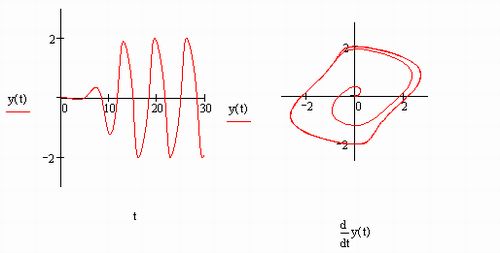
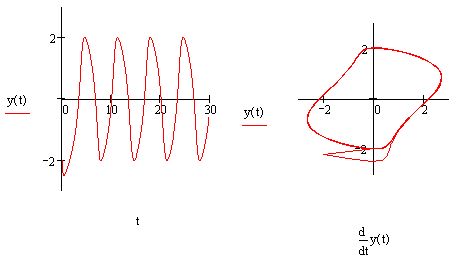
Это еще раз доказывает, что одна и та же система ОДУ с различными коэффициентами может быть жесткой в разной степени. В частности, приведенныйвыше пример генератора Ван дер Поля с параметром ц=5000 - это уже пример жесткой задачи.

В заключение приведем встроенные функции, которые применяются длярешения жестких систем ОДУ не на всем интервале, а только в одной заданной точке ti.
- stiffb(yO,to,ti,acc,F, j, k, s) - метод Булирша-Штера- stiffr (yO,to,ti,acc,F, J,k,s) - метод Розенброка
Имена этих функций пишутся с маленькой буквы, а их действие и наборпараметров полностью аналогичны рассмотренным нами ранее для функций, относящихся к решению в заданной точке нежестких систем(см. разд. 11.3.2). Отличие заключается в специфике применяемого алгоритма и необходимости задания матричной функции якобиана J(t,y).

Глава 10 Содержание Глава 11