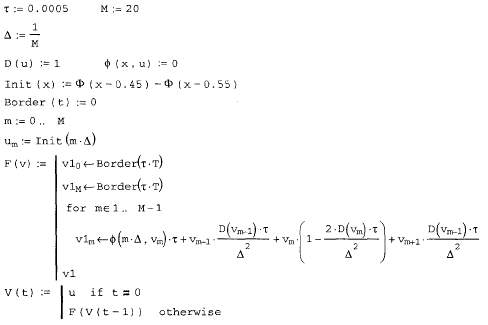• 12.1. Краевые задачи для ОДУ
  • 12.1.1. О постановке краевых задач
  • 12.1.2. Алгоритм стрельбы*
  • 12.1.3. Решение двухточечных краевых задач
  • 12.1.4. Решение краевых задач с дополнительным условием в промежуточной точке
• 12.2. Задачи на собственные значения для ОДУ
• 12.3. Разностные схемы для ОДУ*
  • 12.3.1. О разностном методе решения ОДУ*
  • 12.3.2. Жесткие краевые задачи*
• 12.4. Уравнения в частных производных
  • 12.4.1. Решение уравнения Пуассона
  • 12.4.2. Разностные схемы*
  • 12.4.3. Решение других уравнений в частных производных с помощью функции relax

12.1.1. О постановке краевых задач
Чтобы лучше понять, что из себя представляют краевые задачи, рассмотримих постановочную часть на конкретном физическом примере модели взаимодействия встречных световых пучков. Предположим, что надо определитьраспределение интенсивности оптического излучения в пространстве междуисточником (лазером) и зеркалом, заполненном некоторой средой(рис. 12.1). Будем считать, что от зеркала отражается R-Я часть падающегоизлучения (т. е. его коэффициент отражения равен R), а среда как поглощаетизлучение с коэффициентом ослабления а(х), так и рассеивает его. Причемкоэффициент рассеяния назад равен г(х). В этом случае закон измененияинтенсивности у₀(х) излучения, распространяющегося вправо, и интенсивности yi(x) излучения влево определяется системой двух ОДУ первого порядка:
Для правильной постановки задачи требуется, помимо уравнений, задатьтакое же количество граничных условий. Одно из них будет выражать известную интенсивность излучения ю, падающего с левой границы х=о, авторое - закон отражения на его правой границе x=i:


Рис. 12.1. Модель для постановки краевой задачи
Полученную задачу называют краевой (boundary value problem), поскольку условия поставлены не на одной, а на обеих границах интервала (0,1).И, в связи с этим, их не решить методами предыдущей главы, предназначенными для задач с начальными условиями. Далее для показа возможностей MathCAD будем использовать этот пример с R=I и конкретным видомa(x)=const=i и г(x)=const=o.i, описывающим случай изотропного (не зависящего от координаты х) рассеяния.

Примечание
Модель рис. 12.1 привела к краевой задаче для системы линейных ОДУ. Онаимеет аналитическое решение в виде комбинации экспонент. Более сложные,нелинейные задачи, возможно решить только численно. Нетрудно сообразить,что модель станет нелинейной, если сделать коэффициенты ослабления ирассеяния зависящими от интенсивности излучения. Физически это будет соответствовать изменению оптических свойств среды под действием мощного излучения.


Примечание
Модель встречных световых пучков привела нас к системе уравнений (1), в которые входят производные только по одной переменной х. Если бы мы сталирассматривать более сложные эффекты рассеяния в стороны (а не только вперед и назад), то в уравнениях появились бы частные производные по другимпространственным переменным у и z. В этом случае получилась бы краеваязадача для уравнений в частных производных, решение которой во много раз сложнее ОДУ.

12.1.2. Алгоритм стрельбы*
Для решения краевых задач в MathCAD реализован наиболее популярныйалгоритм, называемый методом стрельбы или пристрелки (shooting method).Он, по сути, сводит решение краевой задачи к решению серии задач Кошис различными начальными условиями. Рассмотрим здесь его основнойпринцип на примере модели (рис. 12.1), а встроенные функции, реализующие этот алгоритм, приведем в следующем разделе.
Суть метода стрельбы заключается в пробном задании недостающих граничных условий на левой границе интервала и решении затем полученной задачи Коши хорошо известными методами (см. гл. 11). В нашем примере нехватает начального условия для yi (о), поэтому сначала зададим ему произвольное значение, например у_х(0)=ю. Конечно, такой выбор не совсем случаен, поскольку из физических соображений ясно, что, во-первых, интенсивность излучения - величина заведомо положительная, и, во-вторых, отраженное излучение должно быть намного меньше падающего. Решениезадачи Коши с помощью функции rkfixed приведено в листинге 12.1.
Листинг 12.1. Решение пробной задачи Коши для модели (12.1-1)

График полученных решений показан на рис. 12.2 (слева). Из него видно,что взятое наугад второе начальное условие не обеспечило выполнение граничного условия при х=1. И понятно, что для лучшего выполнения этогограничного условия следует взять большее значение yi(0). Возьмем, например, yi(0)=is, и вновь решим задачу Коши. Результат показан на том жерис. 12.2 (в центре). Граничное условие выполняется с лучшей точностью,но опять-таки оказалось недостаточным. Для еще одного значения yi(0)=20получается решение, показанное на рис. 12.2 (справа). Из сравнения двухправых графиков легко заключить, что недостающее начальное условиебольше 15, но меньше 20. Продолжая подобным образом "пристрелку" понедостающему начальному условию, возможно отыскать правильное решение краевой задачи.
В этом и состоит принцип алгоритма стрельбы. Выбирая пробные начальные условия (проводя пристрелку) и решая соответствующую серию задачКоши, можно найти то решение системы ОДУ, которое (с заданной точностью) удовлетворит граничному условию (или, в общем случае, условиям)на другой границе расчетного интервала.


Рис. 12.2. Иллюстрация метода стрельбы (листинг 12.1)
Конечно, описанный алгоритм несложно запрограммировать самому, оформив его как решение системы заданных алгоритмически уравнений, выражающих граничные условия на второй границе, относительно неизвестныхпристрелочных начальных условий. Но делать этого нет необходимости, поскольку он оформлен в MathCAD в виде встроенных функций.

12.1.3. Решение двухточечных краевых задач
Решение краевых задач для систем ОДУ методом стрельбы в MathCAD достигается применением двух встроенных функций. Первая предназначена длядвухточечных задач с краевыми условиями, заданными на концах интервала.
sbval(z,xO,xi,o,load,score) - поиск вектора недостающих L начальныхусловий для двухточечной краевой задачи для системы N ОДУ;
 z - вектор размера LXI, присваивающий недостающим начальным условиям (на левой границе интервала) начальные значения;
 хо - левая граница расчетного интервала;
 xi - правая граница расчетного интервала;
 load(xO,z) - векторная функция размера NXI левых граничных условий, причем недостающие начальные условия поименовываются соответствующими компонентами векторного аргумента z;
 score (xi, у) - векторная функция размера LXI, выражающая L правыхграничных условий для векторной функции у в точке xi;
 D(x,y) - векторная функция, описывающая систему N ОДУ, размераNXI и двух аргументов - скалярного х и векторного у. При этом у -это неизвестная векторная функция аргумента х того же размера NXI.
Решение краевых задач в MathCAD, в отличие от большинства остальных операций, реализовано не совсем очевидным образом. В частности, помните, чточисло элементов векторов о и load равно количеству уравнений N, а векторовz, score и результата действия функции sbval - количеству правых граничных условий L. Соответственно, левых граничных условий в задаче должно быть (N-L).
Как видно, функция sbval предназначена не для поиска собственно решения, т. е. неизвестных функций yi (х), а для определения недостающих начальных условий в первой точке интервала, т. е. yt(xO). Чтобы вычислитьYi(x) на всем интервале, требуется дополнительно решить задачу Коши.
Разберем особенности использования функции sbval на конкретном примере (листинг 12.2), описанном выше (см. разд. 12.1.1). Краевая задача состоитиз системы двух уравнений (н=2), одного левого (L=I) и одного правого(N-L=2-i=i) граничного условия.
Листинг 12.2. Решение краевой задачи

Первые три строки листинга задают необходимые параметры задачи и самусистему ОДУ. В четвертой строке определяется вектор z. Поскольку правоеграничное условие всего одно, то недостающее начальное условие тоже одно, соответственно, и вектор z имеет только один элемент z₀. Ему необходимо присвоить начальное значение (мы приняли z₀=io, как в листинге 12.1), чтобы запустить алгоритм стрельбы (см. разд 12.1.2).

Примечание
Начальное значение фактически является параметром численного метода ипоэтому может сильно повлиять на решение краевой задачи.

В следующей строке листинга векторной функции ioad(x,z) присваиваютсялевые граничные условия. Эта функция аналогична векторной переменной,определяющей начальные условия для встроенных функций, решающих задачи Коши. Отличие заключается в записи недостающих условий. Вместоконкретных чисел на соответствующих местах пишутся имена искомых элементов вектора z. В нашем случае вместо второго начального условия стоитаргумент z₀ функции load. Первый аргумент функции load - это точка, вкоторой ставится левое граничное условие. Ее конкретное значение определяется непосредственно в списке аргументов функции sbval.
Следующая строка листинга определяет правое граничное условие, для введения которого используется функция score(х,у). Оно записывается точнотак же, как система уравнений в функции о. Аргумент х функции score аналогичен функции load и нужен для тех случаев, когда граничное условиеявно зависит от координаты х. Вектор score должен состоять из такого жечисла элементов, что и вектор z.
Реализованный в функции sbval алгоритм стрельбы ищет недостающие начальные условия таким образом, чтобы решение полученной задачи Кошиделало функцию score (х, у) как можно ближе к-нулю. Как видно из листинга, результат применения sbval для интервала (0,1) присваивается векторной переменной п. Этот вектор похож на вектор z, только в нем содержатся искомые начальные условия вместо приближенных начальных значений, заданных в z. Вектор и содержит, как и z, всего один элемент I1.С его помощью можно определить решение краевой задачи у(х) (последняястрока листинга). Тем самым, функция sbval сводит решение краевых задачк задачам Коши. График решения краевой задачи показан на рис. 12.3.


Рис. 12.3. Решение краевой задачи


Рис. 12.4. Решение краевой задачидля R=l (листинг 12.2) для R=0
На рис. 12.4 показано решение той же самой краевой задачи, но с другимправым граничным условием, соответствующим R=O, т. е. без зеркала направой границе. В этом случае слабый обратный пучок света образуется исключительно за счет обратного рассеяния излучения от лазера. Конечно,многие из читателей уже обратили внимание, что реальная физическая среда не может создавать такого большого рассеяния назад. Иными словами,более реальны значения г{х)«а(х). Однако, когда коэффициенты в системеОДУ при разных у_± очень сильно (на порядки) различаются, система ОДУстановится жесткой, и функция sbval не может найти решения, выдаваявместо него сообщение об ошибке, гласящей, чаще всего, о невозможностинайти решение, ("Could not find a solution")
Метод стрельбы не годится для решения жестких краевых задач. Поэтому алгоритмы решения жестких ОДУ в MathCAD приходится программировать самому (см. разд. 12.3).

12.1.4. Решение краевых задачс дополнительным условиемв промежуточной точке
Иногда дифференциальные уравнения определяются с граничными условиями не только на концах интервала, но и с дополнительным условием внекоторой промежуточной точке расчетного интервала. Чаще всего такиезадачи содержат данные о негладких в некоторой внутренней точке интервала решениях. Для них имеется встроенная функция bvaifit, также реализующая алгоритм стрельбы.
bvaifit(zl,z2,xO,xl,xf,D,loadl,Ioad2, score) - поиск вектора недостающих граничных условий для краевой задачи с дополнительным условием в промежуточной точке для системы N ОДУ;
 z1 - вектор, присваивающий недостающим начальным условиям налевой границе интервала начальные значения;
 z.2 - вектор того же размера, присваивающий недостающим начальным условиям на правой границе интервала начальные значения;
 хО - левая граница расчетного интервала;
 x1 - правая граница расчетного интервала;
 xf - точка внутри интервала;
 D(x,y) - векторная функция, описывающая систему N ОДУ, размераNXI и двух аргументов - скалярного х и векторного у. При этом у -это неизвестная векторная функция аргумента х того же размера NXI;
 load1(xO,z) - векторная функция размера NXI левых граничных условий, причем недостающие начальные условия поименовываются соответствующими компонентами векторного аргумента z.;
 load2 (xi, z) - векторная функция размера NXI левых граничных условий, причем недостающие начальные условия поименовываются соответствующими компонентами векторного аргумента z;
 score (xf, у) - векторная функция размера NXI, выражающая внутреннее условие для векторной функции у в точке xf.
Обычно функция bvaifit применяется для задач, в которых производнаярешения имеет разрыв во внутренней точке xf. Некоторые из таких задач неудается решить обычным методом пристрелки, поэтому приходится вестипристрелку сразу из обеих граничных точек. В этом случае дополнительноевнутреннее условие в точке xf является просто условием сшивки в ней левого и правого решений. Поэтому для данной постановки задачи оно записывается в форме score (xf, у) :=у.
Рассмотрим действие функции bvaifit на знакомом примере модели взаимодействия пучков света (см. рис. 12.1), предположив, что в промежуткемежду xf=o.5 и xl=i.o находится другая, оптически более плотная среда сдругим коэффициентом ослабления излучения а(х)=з. Соответствующаякраевая задача решена в листинге 12.3, причем разрывный показатель ослабления определяется в его второй строке.
Листинг 12.3. Краевая задача с граничным условием в промежуточной точке

Система уравнений и левое краевое условие вводится так же, как и в предыдущем листинге для функции sbvai. Обратите внимание, что таким же образом записано и правое краевое условие. Для того чтобы ввести условие отражения на правой границе, пришлось определить еще один неизвестныйпристрелочный параметр z2₀. Строка листинга, в которой определена функция score, задает условие стрельбы - сшивку двух решений в точке xf.В самой последней строке листинга выдан ответ - определенные численнымметодом значения обоих пристрелочных параметров, которые объединены ввектор II (мы применили в предпоследней строке операцию транспонирования, чтобы результат получился в форме вектора, а не матрицы-строки).
Для корректного построения графика решения лучше составить его из двух частей - решения задачи Коши на интервале (xO,xf) и другой задачи Кошидля интервала (xf,xi). Реализация этого способа приведена в листинге 12.4,который является продолжением листинга 12.3. В последней строке лис тинга 12.4 выведено значение второй искомой функции на правой границе интервала. Всегда полезно проконтролировать, что оно совпадает с соответствующим пристрелочным параметром (выведенном в последней строкелистинга 12.3).
Листинг 12.4. Решение краевой задачи (продолжение листинга 12.3)

Решение краевой задачи приведено на рис. 12.5. С физической точки зренияестественно, что интенсивность света уменьшается быстрее по мере распространения в более плотной среде в правой половине расчетного интервалаВ средней точке xf=o.5, как и ожидалось, производные обоих решенийимеют разрыв.

Примечание
Еще один пример решения краевых задач с разрывными коэффициентами ОДУ приведен в справочной системе MathCAD.



Рис. 12.5. Решение краевой задачи с разрывом в xf=0.5 (листинги 12.3-12.4)
Ради справедливости необходимо заметить, что разобранную краевую задачулегко решить и с помощью функции sbval, заменив в листинге 12.2 зависимость а(х) на третью строку листинга 12.3. В этом случае листинг 12.2 даст в точности тот же ответ, что показан на рис. 12.5. Однако в определенныхслучаях (в том числе из соображений быстроты расчетов) удобнее использовать функцию bvalfit, т. е. вести пристрелку с обеих границ интервала.

Совет
Если вы имеете дело с подобными уравнениями, попробуйте сначала решитьих как обычную краевую задачу с помощью более надежной и легкой в применении функции sbval.

12.2. Задачи на собственные значениядля ОДУ
Задачи на собственные значения - это краевые задачи для системы ОДУ,в которой правые части зависят от одного или нескольких параметров Л..Значения этих параметров неизвестны, а решение краевой задачи существует только при определенных X_k, которые называются собственными значениями (eigenvalues) задачи. Решения, соответствующие этим А*, называютсобственными функциями (eigenfunctions) задачи. Правильная постановка таких задач требует формулировки количества граничных условий, равногосумме числа уравнений и числа собственных значений. Физическими примерами задач на собственные значения являются, например, уравнение колебаний струны, уравнение Шредингера в квантовой механике, уравненияволн в резонаторах и многие другие.
С вычислительной точки зрения, задачи на собственные значения очень похожи на рассмотренные выше краевые задачи. В частности, для многих изних так же применим метод стрельбы (см. разд. 12.1.2). Отличие заключаетсяв пристрелке не только по недостающим левым граничным условиям, ноеще и по искомым собственным значениям. В MathCAD для решения задачна собственные значения используются те же функции sbval и bvalfit.В их первый аргумент, т. е. вектор, присваивающий начальные значениянедостающим начальным условиям, следует включить и начальное приближение для собственного значения.
Рассмотрим методику решения на конкретном примере определения собственных упругих колебаний струны. Профиль колебаний струны у(х) описывается линейным дифференциальным уравнением второго порядка
Если струна закреплена на обоих концах, то граничные условия задаются в виде у(0)=у(1)=о. Сформулированная задача является частным случаем задачи Штурма-Лиувилля. Поскольку решается сие тема двух ОДУ, содержащая одно собственное значение А,, то по идее задачатребует задания трех (2+1) условий. Однако, как легко убедиться, уравнениеколебаний струны - линейное и однородное, поэтому в любом случае решение у(х) будет определено с точностью до множителя. Это означает, чтопроизводную решения можно задать произвольно, например у' (0)=1, что ибудет третьим условием. Тогда краевую задачу можно решать как задачуКоши, а пристрелку вести только по одному параметру - собственномузначению.
Процедура поиска первого собственного значения представлена в листинге 12.5.
Листинг 12.5. Решение задачи о собственных колебаниях струны

В первых двух строках листинга определяются функции, входящие в задачу,в том числе р¹ (х) :=о, и границы расчетного интервала (0,1). В третьейстроке дается начальное приближение к собственному значению Х₀, в четвертой вводится система ОДУ. Обратите внимание, что она состоит не издвух, а из трех уравнений. Первые два из них определяют эквивалентную (1)систему ОДУ первого порядка, а третье необходимо для задания собственного значения в виде еще одного компонента у₂ искомого вектора у. Поскольку, по определению, собственное значение постоянно при всех х, тоего производная должна быть приравнена нулю, что отражено в последнемуравнении. Важно также, что во втором из уравнений собственное значениезаписано как у₂, поскольку является одним из неизвестных.
В следующих двух строках листинга задается левое граничное условие,включающее и недостающее условие на собственное значение для третьего уравнения, и правое граничное условие у₀=о. В предпоследней строке листинга обычным образом применяется функция sbval, а в последней выводится результат ее работы вместе с известным- аналитически собственнымзначением п²-я². Как легко убедиться, мы нашли первое собственное значение для п=1, а чтобы найти другие собственные значения, необходимо задатьдругие начальные приближения к ним (в третьей строке листинга 12.5). Например, выбор Л₀=50 приводит ко второму собственному значению 2²-пи², аА,о=100 - к третьему з²-пи².
Чтобы построить график соответствующей собственной функции, надо добавить в листинг строку, программирующую решение задачи Коши, например, такую: U:=rkfixed(ioad(a,A),a,b,IOO,D). Полученные кривые показанына рис. 12.6 в виде коллажа трех графиков, рассчитанных для трех собственных значений.

Примечание
Примеры решения нескольких задач на собственные значения можно найти в Центре Ресурсов MathCAD.



Рис. 12.6. Первые трисобственные функции задачи колебаний струны (коллажтрех графиков)

12.3.1. О разностном методе решения ОДУ*
Разберем идею разностного метода решения .краевых задач на примеревзаимодействия световых пучков (см. рис. 12.1), переобозначив в системе(12.1-1) интенсивность излучения вправо на Y, а интенсивность излучениявлево на у (просто в целях удобства, чтобы не писать индекс). Суть методазаключается в покрытии расчетного интервала сеткой из N точек. Тем самымопределяются (N-i) шагов (рис. 12.7). Затем надо заменить дифференциальные уравнения исходной краевой задачи аппроксимирующими их уравнениями в конечных разностях, выписав соответствующие разностные уравнения для каждого 1-го шага. В нашем случае достаточно просто заменитьпервые производные из (12.1-1) их разностными аналогами (такой методназывается еще методом Эйлера):


Рис. 12.7. Сетка, покрывающая расчетный интервал

Примечание
Существует множество способов аппроксимации дифференциальных уравнений разностными. От выбора конкретного варианта зависит не только простота,быстрота и удобство вычислений, но и сама возможность получения правильного ответа.

Получилась система (по числу шагов) 2-(м-1) разностных линейных алгебраических уравнений с 2-N неизвестными YI и yi. Для того чтобы она имелаединственное решение, надо дополнить число уравнений до 2-м. Это можносделать, записав в разностном виде оба граничных условия:
Y₀=1O, y_N=R-Y_N.
Сформированная полная система алгебраических уравнений называется разностной схемой, аппроксимирующей исходную краевую задачу. Обратитевнимание, что правые части разностных уравнений системы на каждомшаге записаны для левой границы шага. Такие разностные схемы называютявными, т. к. все значения Y_I+I и y_i+i находятся в левой части уравнений. Полученную явную разностную схему легко записать в матричной форме
A._Z=B,
где z - неизвестный вектор, получающийся объединением векторов Y и у.Решив систему (3), мы получим решение краевой задачи.

Примечание
На самом деле, все несколько сложнее, поскольку, вообще говоря, необходимоеще доказать, что, во-первых, разностная схема действительно аппроксимирует дифференциальные уравнения и, во-вторых, при м-*» разностное решениедействительно сходится к дифференциальному.

Процесс решения системы разностных уравнений называют также реализацией разностной схемы. Программа, которая решает рассматриваемую краевую задачу разностным методом, приведена в листинге 12.6.
Листинг 12.6. Реализация явной разностной схемы

Дадим минимальные комментарии, надеясь, что заинтересовавшийся читатель с карандашом в руках разберется в порядке индексов и соответствии матричных элементов, а возможно, составит и более удачную программу.
В первой строке листинга определяются функции и константы, входящие вмодель, во второй задается число точек сетки N=5 и ее равномерный шаг.Следующие две строки определяют матричные коэффициенты, аппроксимирующие уравнения для Y_I} а пятая и шестая - для у^. Седьмая и восьмаястроки листинга задают соответственно левое и правое граничное условие, астроки с девятой по одиннадцатую - правые части системы (3). В следую щей строке завершается построение матрицы л вырезанием из нее левого нулевого столбца. В предпоследней строке листинга применена встроенная функция isoive для решения системы , а в последней выведены рассчитанные ею неизвестные граничные значения. Графики решения приведенына рис. 12.8, причем первые N элементов итогового вектора есть вычисленное излучение вперед, а последние N элементов - излучение назад.


Рис. 12.8. Решение краевой задачи разностным методом(листинг 12.6)
Как мы увидели, реализация в MathCAD разностных схем вполне возможнаи не слишком трудоемка - предложенная программа состоит всего из двухдесятков математических выражений. Конечно, для их написания требуетсяи время, и часто кропотливые расчеты, но, собственно, в этом и состоитработа математика. Кстати говоря, при небольшом числе шагов, расчеты поразностным схемам не требуют существенного времени (программа, приведенная в листинге 12.6, работает быстрее, чем метод стрельбы, встроенный вфункцию sbval). Существуют, кроме того, весьма очевидные для многихчитателей пути ускорения расчетов, связанные с применением более подходящих методов решения систем линейных уравнений с разреженной матрицей.

12.3.2. Жесткие краевые задачи*
Один из случаев, когда применение разностных схем может быть очень полезным, связан с решением жестких краевых задач (подробнее о жесткихОДУ читайте в гл. 11). В частности, рассматриваемая задача о встречныхсветовых пучках становится жесткой при увеличении коэффициента ослабления а(х) в несколько десятков раз. Например, при попытке решить ее са(х) :=100 с помощью листинга 12.2, вместо ответа выдается сообщение обошибке "Can't converge to a solution. Encountered too many integration steps"(He сходится к решению. Слишком много шагов интегрирования). Это инеудивительно, поскольку жесткие системы характерны тем, что требуютисключительно малого значения шага в стандартных алгоритмах.
Для жестких задач неприменимы и явные разностные схемы, о которых рассказывалось в предыдущем разделе (см. разд. 12.3.1). Результат расчетов попрограмме листинга 12.6, например с а(х) :=20°(рис. 12.9), дает характернуюдля неустойчивых разностных схем "разболтку" - колебания нарастающейамплитуды, не имеющие ничего общего с реальным решением.


Рис. 12.9. Неверное решение жесткой краевой задачипо неустойчивой явной разностной схеме
Выходом из положения будет использование неявных разностных схем.Применительно к нашей задаче достаточно заменить правые части уравнений (1) значениями не на левой, а на правой границе каждого шага:
Граничные условия, конечно, можно оставить в том же виде (2). Посколькумы имеем дело с линейными дифференциальными уравнениями, то и схему(4) легко будет записать в виде матричного равенства (3), перегруппировывая соответствующим образом выражение (4) и приводя подобные слагаемые. Разумеется, полученная матрица А будет иной, нежели матрица А дляявной схемы (1). Поэтому и решение (реализация неявной схемы) можетотличаться от изображенного на рис. 12.9 результата расчетов по явной схеме. Программа, составленная для решения системы (4), приведена в листинге 12.7.
Листинг 12.7. Реализация неявной разностной схемыдля жесткой краевой задачи

Не будем специально останавливаться на обсуждении листинга 12.7, поскольку он почти в точности повторяет предыдущий листинг. Отличие заключается лишь в формировании матрицы А другим способом, согласнонеявной схеме. Решение, показанное на рис. 12.10, демонстрирует, что произошло "небольшое чудо": "разболтка" исчезла, а распределение интенсивностей стало физически предсказуемым. Обратите внимание, что (из-за взятого нами слишком большого коэффициента ослабления излучения) отраженный пучок света имеет очень маленькую интенсивность, и ее пришлосьпостроить на графике с увеличением в тысячу раз.


Рис. 12.10. Решение краевой задачи разностным методом(листинг 12.7)

Примечание
Все примеры, рассмотренные в этом разделе, связаны с краевыми задачамидля линейных ОДУ. Благодаря линейности исходных уравнений и система разностных уравнений получалась линейной. Если же дифференциальные урав нения нелинейные, то решение их разностным методом существенно усложняется. Разбор соответствующих программ MathCAD выходит далеко за пределыданной книги. Но читатель, заинтересовавшийся примером со световыми пучками, может найти решение нелинейной задачи, описывающей эффект разогрева светом среды, на сайте автора

12.4.1. Решение уравнения Пуассона
Двумерное уравнение Пуассона - пример уравнения в частных производных эллиптического типа, включающее в себя вторые производные функциит(х,у) по двум пространственным переменным:
Уравнение Пуассона описывает, например, распределение электростатического поля т(х,у) в двумерной области с плотностью заряда f(x,y), илистационарное распределение температуры т(х,у) на плоскости, в которойимеются источники (или поглотители) тепла с интенсивностью f(x,y).Именно в последней физической интерпретации и будем далее рассматривать уравнение Пуассона (поэтому мы и обозначили искомую функциюсимволом т).
Корректная постановка краевой задачи для уравнения Пуассона требует задания граничных условий. В MathCAD решение ищется на плоской квадратной области, состоящей из <м+1)х(м+1) точек. Поэтому граничные условия должны быть определены пользователем для всех четырех сторон упомянутого квадрата. Самый простой вариант - это нулевые граничныеусловия, т. е. постоянная температура по всему периметру расчетной области. В таком случае можно использовать встроенную функцию multigrid.
- multigrid(F,ncycie) - матрица решения уравнения Пуассона размера(м+1)х(м+1) на квадратной области с нулевыми граничными условиями;
 F- матрица размера (м+1)х<м+1), задающая правую часть уравненияПуассона;
 ncyde - параметр численного алгоритма (количество циклов в пределах каждой итерации).
Сторона квадрата расчетной области должна состоять из М=2^П точек, где п -целое число.
Параметр численного метода ncyde в большинстве случаев достаточно взятьравным 2. Листинг 12.8 содержит пример использования функции multigridдля расчета краевой задачи на области ззхзз точки и точечным источникомтепла в месте, задаваемом координатами (15,20) внутри этой области.
Листинг 12.8. Решение уравнения Пуассонас нулевыми граничными условиями

В первой строке листинга задается значение м=32, в двух следующих строкахсоздается матрица правой части уравнения Пуассона, состоящая из всех нулевых элементов, за исключением одного, задающего расположение источника. В последней строке матрице с присваивается результат действияфункции multigrid. Обратите внимание, первый ее аргумент сопровождается знаком "минус", что соответствует записи правой части уравнения Пуассона . Графики решения показаны на рис. 12.11 и 12.12 в виде трехмерной поверхности и линий уровня, соответственно.
В более сложных случаях, например, для решения краевой задачи с ненулевыми условиями на границах, следует использовать другую встроеннуюфункцию relax, имеющуюся в MathCAD.
- relax(a,b,c,d,e,F,v,) - матрица решения дифференциальногоуравнения в частных производных на квадратной области, полученного спомощью алгоритма релаксации для метода сеток;
 a,b,c,d,e- квадратные матрицы коэффициентов разностной схемы,аппроксимирующей дифференциальное уравнение;
 F - квадратная матрица, задающая правую часть дифференциальногоуравнения;
 v - квадратная матрица граничных условий и начального приближения к решению;
 rjac - параметр численного алгоритма (спектральный радиус итераций Якоби).


Рис. 12.11. График поверхности решения уравнения Пуассона(листинг 12.8)


Рис. 12.12. График линий уровня решения уравнения Пуассона(листинг 12.8)
Параметр численного алгоритма характеризует скорость сходимости итераций. Он должен быть числом от о до 1. В матрице граничных условий v необходимо задать только граничные элементы, исходя из значения краевыхусловий по периметру расчетной области. Прочие (внутренние) элементыэтой матрицы служат для задания начального приближения к решению.Суть алгоритма релаксации сводится к тому, что в ходе итераций происходит проверка уравнений и соответствующая коррекция значений искомойфункции в каждой точке. Если начальное приближение выбрано удачно, томожно надеяться, что алгоритм сойдется ("срелаксирует") к правильномурешению.
Все матрицы, задающие как коэффициенты разностной схемы а,ь, с, d, e, граничные условия v, так и само решение F, должны иметь одинаковый размер(м+1)х(м+1), соответствующий размеру расчетной области. При этом целоечисло м обязательно должно быть степенью двойки: м=2^п.
Решение уравнения Пуассона с тремя источниками разной интенсивностипри помощью функции relax приведено в листинге 12.9.
Листинг 12.9. Решение уравнения Пуассона с помощью функции relax

Первые три строки имеют тот же смысл, что и в предыдущем листинге.Только вместо одного источника тепла взято их другое распределение -один сильный источник, один более слабый и один сток тепла. В следующих шести строках задаются коэффициенты разностной схемы. Отложим ихобсуждение до последнего раздела этой главы, ограничившись утверждением, что для решения уравнения Пуассона коэффициенты должны быть взяты именно такими, как показано в листинге 12.9. В предпоследней строкезадана матрица нулевых граничных условий и нулевых начальных приближений, а в последней матрице с присваивается результат действия функцииrelax. График полученного решения в виде линий уровня показан напие 12.13.


Рис. 12.13. Решение уравнения Пуассона с помощьюфункции relax (листинг 12.9)

12.4.2. Разностные схемы
С помощью встроенных функций можно решить только самые простыеуравнения в частных производных. Как правило, пользователи, которымприходится исследовать эти уравнения, имеют хорошее представление о соответствующих численных алгоритмах, чаще всего связанных с расчетами поразностным схемам. Поэтому ограничимся демонстрацией программы, которая реализует метод сеток для уравнения теплопроводности (или диффузиитепла)'.
Это уравнение параболического типа, содержащее первую производную повремени t и вторую по пространственной координате х. Оно описывает динамику температуры T(x,t) в присутствии источников тепла <j>(x,T,t), например, при нагреве металлического стержня. Для уравнения явная разностная схема имеет вид где коэффициент к характеризует отношение шагов разностной схемы попространству и времени . Для построения разностной схемы мы покрыли расчетную область (x,t) сеткой и использовали для разностной аппроксимации уравнения (2) конфигурацию узлов (шаблон), показанную на рис. 12.14 (о принципе построения разностных схем см. разд. 12.3.1).Рядом с каждой точкой шаблона приведены значения коэффициентов призначениях искомой функции в соответствующих узлах сетки, которые получаются после приведения в схеме (3) подобных слагаемых.


Рис. 12.14. Шаблон аппроксимации уравнения теплопроводности
Реализация разностной схемы для модели без источников тепла 0(x,T,t)=o приведена в листинге 12.10. В его первых трех строках заданышаги (т, и Д) по временной и пространственной переменным и коэффициент диффузии о, равный единице. В следующих двух строках заданы начальные (нагретый центр области) и граничные (постоянная температура на краях) условия соответственно. Затем приводится возможное программное решениеразностной схемы, причем функция пользователя v(t) задает вектор распределения искомой температуры в каждый момент времени, задаваемый целым числом t.
Листинг 12.10. Решение линейного уравнения теплопроводности

Начальное распределение температуры вдоль расчетной области и решениедля двух моментов времени показано на рис. 12.15 сплошной, пунктирной иштриховой линиями соответственно. Физически такое поведение вполнеестественно - с течением времени тепло из более нагретой области перетекает в менее нагретую, а зона изначально высокой температуры остывает иразмывается.
Намного более интересные решения можно получить для нелинейногоуравнения теплопроводности, например, с нелинейным источником тепла<i>(x,t)=io³-(т-т³). Если задать его в таком виде в третьей строке листинга 12.10, то получится решение в форме тепловых фронтов, распространяющихся в обе стороны от зоны первичного нагрева (рис. 12.16). Еще болеенеожиданные решения возможны при нелинейности также и коэффициентадиффузии. Например, если взять о(х,т)=т², a 0(x,t)=10³-T³-⁵, то вы сможетенаблюдать эффект горения среды, локализованный в области ее первичногонагрева. Читателю предлагается поэкспериментировать с этим и другими нелинейными вариантами уравнения теплопроводности. Существенно, чтотакие интересные результаты удается получить лишь численно, а в MathCAD только с применением элементов программирования.


Рис. 12.15. Решение линейного уравнения теплопроводности(листинг 12.10)


Рис. 12.16. Решение уравнения теплопроводности с нелинейным источником(тепловой фронт)

12.4.3. Решение других уравнений в частныхпроизводных с помощью функции relax
Несмотря на отсутствие сведений в справочной системе MathCAD о решении других линейных дифференциальных уравнений в частных производных, кроме уравнения Пуассона, сделать это возможно с помощью той жефункции relax (см. разд. 12.4.1). Для этого нужно правильным образом задать коэффициенты разностной схемы.
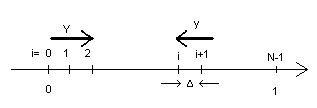
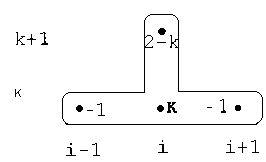
Начнем с пояснения выбора этих коэффициентов (см. листинг 12.9) дляуравнения Пуассона. Согласно идеям предыдущего раздела, уравнение Пуассона (1) может быть записано в разностной форме при помощи шаблона"крест" (рис. 12.17). В этом случае, после приведения подобных слагаемых вразностных уравнениях коэффициенты разностной схемы будут такими, какпоказано возле узлов шаблона на этом рисунке (аналогичные коэффициенты для уравнения теплопроводности см. на рис. 12.14). Теперь, если высравните полученные числа с константами, которые присвоены элементамматриц-аргументов функции relax (см. листинг 12.9), то увидите, что оникак раз и описывают вычисленные нами только что коэффициенты разностной схемы "крест".


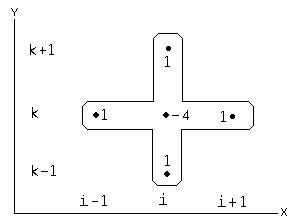
Рис. 12.17. Шаблон аппроксимации уравнения Пуассона "крест"
Таким образом, нетрудно сообразить, что с помощью встроенной функцииrelax можно решать и другие линейные дифференциальные уравнения вчастных производных, которые можно аппроксимировать схемой типа"крест" или схемой, являющейся ее составной частью. Например, возможнареализация явной схемы для однородного уравнения теплопроводности(см. разд. 12.4.2). Для этого требуется задать коэффициенты, показанные нашаблоне (см. рис. 12.14), в аргументах функции relax (листинг 12.11).
Листинг 12.11. Решение уравнения теплопроводности С помощью функции relax

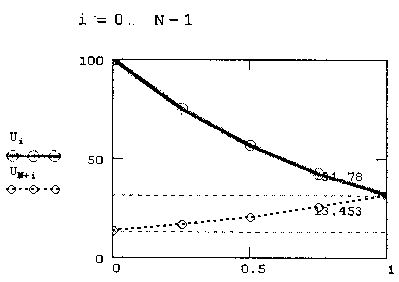
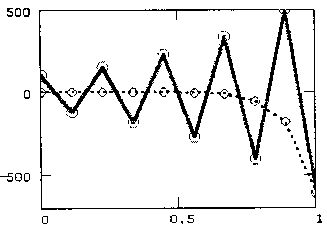
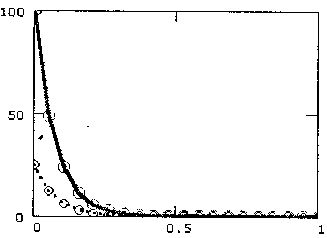
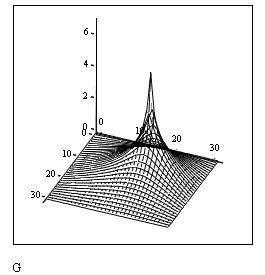
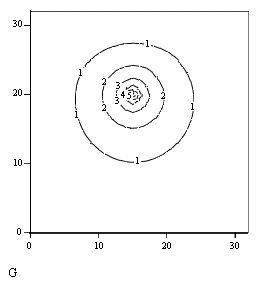
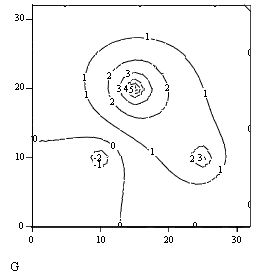
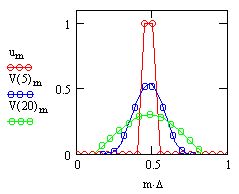
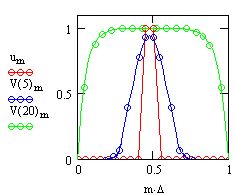
В остальном, программа работает точно так же, как представленная на листинге 12.9. Результат ее действия показан на рис. 12.18 в виде трехмернойповерхности. Если сравнить рис. 12.18 с рис. 12.15, полученным при расчетах по запрограммированной разностной схеме, то в графиках рис. 12.15 нетрудно узнать сечения этой поверхности плоскостями t=const.


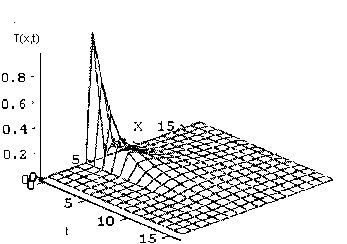
Рис. 12.18. Решение уравнения теплопроводности с помощью функции relax (листинг 12.11)
В заключение разговора об уравнениях в частных производных, нельзя несказать несколько слов об их визуализации. Результат решения динамических уравнений (зависящих от времени t) выглядит намного эффектнее,если будет представлен в виде анимации. Для создания анимационных роликов расчетное время следует выразить через константу FRAME и затем применить команду View / Animate (Вид / Анимация) (как об этом рассказано вразд. "Создание анимации"гл. 15).

Глава 11 Содержание Глава 13