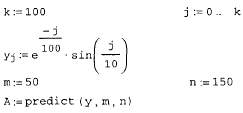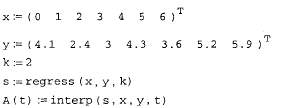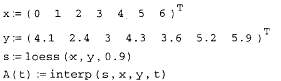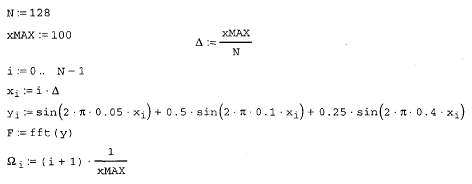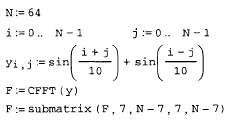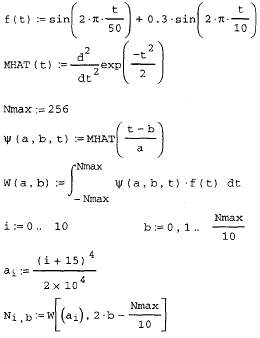• 14.1. Интерполяция
  • 14.1.1. Линейная интерполяция
  • 14.1.2. Кубическая сплайн-интерполяция
  • 14.1.3. Полиномиальная сплайн-интерполяция
  • 14.1.4. Экстраполяция функцией предсказания
  • 14.1.5. Многомерная интерполяция
• 14.2. Регрессия
  • 14.2.1. Линейная регрессия
  • 14.2.2. Полиномиальная регрессия
  • 14.2.3. Регрессия специального вида
  • 14.2.4. Регрессия общего вида
• 14.3. Сглаживание и фильтрация
  • 14.3.1. Встроенные функции для сглаживания
  • 14.3.2. Скользящее усреднение*
  • 14.3.3. Устранение тренда*
  • 14.3.4. Полосовая фильтрация*
• 14.4. Интегральные преобразования
  • 14.4.1. Преобразование Фурье
  • 14.4.2. Вейвлетное преобразование

14.1.1. Линейная интерполяция
Самый простой вид интерполяции - линейная, которая представляет искомую зависимость А(х) в виде ломаной линии. Интерполирующая функцияА(х) состоит из отрезков прямых, соединяющих точки (рис. 14.2).


Рис. 14.2. Линейная интерполяция (листинг 14.1)
Для построения линейной интерполяции служит встроенная функция linterp (листинг 14.1).
- linterp(х, у,t) - функция, аппроксимирующая данные векторов х и укусочно-линейной зависимостью;
 х - вектор действительных данных аргумента;
 у - вектор действительных данных значений того же размера;
 t - значение аргумента, при котором вычисляется интерполирующаяфункция.
Элементы вектора х должны быть определены в порядке возрастания, т. е. Х1<Х2<Хз<. . . <XN.
Листинг 14.1. Линейная интерполяция

Как видно из листинга, чтобы осуществить линейную интерполяцию, надовыполнить следующие действия:
1. Введите векторы данных х и у (первые две строки листинга).
2. Определите функцию linterp (х, у, t).
3. Вычислите значения этой функции в требуемых точках, например linterp(x,y,2.4) =3.52, или linterp(х,у,6) =5.9, или постройте ее график,как показано на рис. 14.2.

Примечаниe
Обратите внимание, что функция A(t) на графике имеет аргумент t, а не х.Это означает, что функция A(t) вычисляется не только при значениях аргумента (т. е. в семи точках), а при гораздо большем числе аргументов в интервале(0,6), что автоматически обеспечивает MathCAD. Просто в данном случае этиразличия незаметны, т. к. при обычном построении графика функции А(х) отвекторного аргумента х (рис. 14.3) MathCAD, по умолчанию, соединяет точкиграфика прямыми линиями (т. е. скрытым образом осуществляет их линейнуюинтерполяцию).



Рис. 14.3. Обычное построение графика функции от векторной переменной х(листинг 14.1)

14.1.2. Кубическая сплайн-интерполяция
В большинстве практических приложений желательно соединить экспериментальные точки не ломаной линией, а гладкой кривой. Лучше всего дляэтих целей подходит интерполяция кубическими сплайнами, т. е. отрезкамикубических парабол (рис. 14.4).
- interp(s,x,y,t) - функция, аппроксимирующая данные векторов х и укубическими сплайнами;
 s - вектор вторых производных, созданный одной из сопутствующих функций cspline, pspline или Ispline;
 х - вектор действительных данных аргумента, элементы которогорасположены в порядке возрастания;
 у - вектор действительных данных значений того же размера;
 t - значение аргумента, при котором вычисляется интерполирующаяфункция.


Рис. 14.4. Сплайн-интерполяция (см. листинг 14.2)
Сплайн-интерполяция в MathCAD реализована чуть сложнее линейной. Перед применением функции interp необходимо предварительно определитьпервый из ее аргументов - векторную переменную s. Делается это при помощи одной из трех встроенных функций тех же аргументов (х,у).
- lspiine(x,y) - вектор значений коэффициентов линейного сплайна;- pspiine(x,y) - вектор значений коэффициентов квадратичного сплайна;- cspiine(x,y) - вектор значений коэффициентов кубического сплайна; х,у - векторы данных.
Выбор конкретной функции сплайновых коэффициентов влияет на интерполяцию вблизи конечных точек интервала. Пример сплайн-интерполяцииприведен в листинге 14.2.
Листинг 14.2. Кубическая сплайн-интерполяция

Смысл сплайн-интерполяции заключается в том, что в промежутках между точками осуществляется аппроксимация в виде зависимости A(t) ==a-t³+b-t²+c-t+d. Коэффициенты a,b,c,d рассчитываются независимо длякаждого промежутка, исходя из значений yi в соседних точках. Этот процессскрыт от пользователя, поскольку смысл задачи интерполяции состоит ввыдаче значения A(t) в любой точке t (рис. 14.4).
Рис. 14.5. Сплайн-интерполяция с выбором коэффициент овлинейного сплайна lspline


Рис. 14.6. Ошибочное построение графика сплайн-интерполяции(см. листинг 14.2)


Чтобы подчеркнуть различия, соответствующие разным вспомогательнымфункциям cspline, pspline, Ispline, покажем результат действия листинга 14.2 при замене функции cspiine в предпоследней строке на линейнуюIspline (рис. 14.5). Как видно, выбор вспомогательных функций существен но влияет на поведение A(t) вблизи граничных точек рассматриваемого интервала (0,6) и особенно разительно меняет результат экстраполяции данных за его пределами.
В заключение, остановимся на уже упоминавшейся в предыдущем разделераспространенной ошибке при построении графиков интерполирующейфункции (см. рис. 14.3). Если на графике, например, являющемся продолжением листинга 14.2, задать построение функции А(х) вместо A(t), то будет получено просто соединение исходных точек ломаной (рис. 14.6). Такпроисходит потому, что в промежутках между точками вычисления интерполирующей функции не производятся.

14.1.3. Полиномиальная сплайн-интерполяция
Более сложный тип интерполяции - так называемая интерполяция В-сплайнами. В отличие от обычной сплайн-интерполяции (см. разд. 14.1.2), сшивкаэлементарных В-сплайнов производится не в точках x_i; а в других точках u_i,координаты которых предлагается ввести пользователю. Сплайны могутбыть полиномами 1, 2 или з степени (линейные, квадратичные или кубические). Применяется интерполяция В-сплайнами точно так же, как и обычная сплайн-интерполяция, различие состоит только в определении вспомогательной функции коэффициентов сплайна.
- interp(s,x,y,t) - функция, аппроксимирующая данные векторов х и ус помощью В-сплайнов;
- bspiine(x,y,u,n) - вектор значений коэффициентов В-сплайна;
 s - вектор вторых производных, созданный функцией bspline;
 х - вектор действительных данных аргумента, элементы которогорасположены в порядке возрастания;
 у - вектор действительных данных значений того же размера;
 t - значение аргумента, при котором вычисляется интерполирующаяфункция;
 u - вектор значений аргумента, в которых производится сшивкаВ-сплайнов;
 n - порядок полиномов сплайновой интерполяции (l, 2 или 3).

Примечание
Размерность вектора и должна быть на 1, 2 или з меньше размерности векторов х и у. Первый элемент вектора и должен быть меньше или равен первомуэлементу вектора х, а последний элемент и - больше или равен последнемуэлементу х.

Интерполяция В-сплайнами иллюстрируется листингом 14.3 и рис. 14.7.
Листинг 14.3. Интерполяция В-сплайнами



Рис. 14.7. В-сплайн-интерполяция (листинг 14.3)

14.1.4. Экстраполяция функцией предсказания
Все рассмотренные выше (см. разд. 14.1.1-14.1.3) функции осуществлялиэкстраполяцию данных за пределами их интервала с помощью соответствующей зависимости, основанной на анализе расположения нескольких исходных точек на границах интервала. В MathCAD имеется более развитыйинструмент экстраполяции, который учитывает распределение данных вдольвсего интервала. В функцию predict встроен линейный алгоритм предсказания поведения функции, основанный на анализе, в том числе осцилляции.
- predict (y,m,n) - функция предсказания вектора, экстраполирующеговыборку данных;
 у - вектор действительных значений, взятых через равные промежутки значений аргумента;
 m - количество последовательных элементов вектора у, согласно которым строится экстраполяция;
 n - количество элементов вектора предсказаний.
Пример использования функции предсказания на примере экстраполяцииосциллирующих данных у₃ с меняющейся амплитудой приведен в листинге 14.4. Полученный график экстраполяции, наряду с самой функцией, показан на рис. 14.8. Аргументы и принцип действия функции predict отличаются от рассмотренных выше встроенных функций интерполяции-экстраполяции. Значений аргумента для данных не требуется, поскольку поопределению функция действует на данные, идущие друг за другом с равномерным шагом. Обратите внимание, что результат функции predict вставляется "в хвост " исходных ланных.
Листинг 14.4. Экстраполяция при помощи функции предсказания



Рис. 14.8. Экстраполяция при помощи функции предсказания (листинг 14.4)
Как видно из рис. 14.9, функция предсказания может быть полезна при экстраполяции данных на небольшие расстояния. Вдали от исходных данныхрезультат часто бывает неудовлетворительным. Кроме того, функция predictхорошо работает в задачах анализа подробных данных с четко прослеживающейся закономерностью (типа рис. 14.8), в основном осциллирующегохарактера.
Если данных мало, то предсказание может оказаться бесполезным. В листинге 14.5 приведена экстраполяция небольшой выборки данных (из примеров, рассмотренных в предыдущих разделах). Соответствующий результатпоказан на рис. 14.9 для различных крайних точек массива исходных данных, для которых строится экстраполяция.
Листинг 14.5. Экстраполяция при помощи функции предсказания



Рис. 14.9. Работа функции предсказания в случае малого количества данных (листинг 14.5)

14.1.5. Многомерная интерполяция
Двумерная сплайн-интерполяция приводит к построению поверхностиz(x,y), проходящей через массив точек, описывающий сетку на координат ной плоскости (х,у). Поверхность создается участками двумерных кубических сплайнов, являющихся функциями (х,у) и имеющих непрерывныепервые и вторые производные по обеим координатам.
Многомерная интерполяция строится с помощью тех же встроенных функций, что и одномерная (см. разд. 14.1.2), но имеет в качестве аргументов невекторы, а соответствующие матрицы. Существует одно важное ограничение, связанное с возможностью интерполяции только квадратных NXN массивов данных.
- interp(s,x,z,v) - скалярная функция, аппроксимирующая данные выборки двумерного поля по координатам х и у кубическими сплайнами;
 s - вектор вторых производных, созданный одной из сопутствующих функции cspline, pspline ИЛИ Ispline
 х - матрица размерности Nx2, определяющая диагональ сетки значений аргумента (элементы обоих столбцов соответствуют меткам х и уи расположены в порядке возрастания);
 z - матрица действительных данных размерности NXN;
 v - вектор из двух элементов, содержащий значения аргументов х и у,для которых вычисляется интерполяция.

Примечание
Вспомогательные функции построения вторых производных имеют те же матричные аргументы, что и interp: Ispline (X, Y), pspline (X, Y), cspline (X, Y).

Пример исходных данных приведен на рис. 14.10 в виде графика линийуровня, программная реализация двумерной интерполяции показана в листинге 14.6, а ее результат - на рис. 14.11.
Листинг 14.6. Двумерная интерполяция



Рис. 14.10. Исходное двумерное поле данных(листинг 14.6)


Рис. 14.11. Результат двумерной интерполяции(листинг 14.6)

14.2.1. Линейная регрессия
Самый простой и наиболее часто используемый вид регрессии - линейная.Приближение данных (xi,yi) осуществляется линейной функциейу(х)=b+а-х. На координатной плоскости (х,у) линейная функция, как известно, представляется прямой линией (рис. 14.12). Еще линейную регрессию часто называют методом наименьших квадратов, поскольку коэффициенты а и b вычисляются из условия минимизации суммы квадратов ошибок

Примечание
Чаще всего, такое же условие ставится и в других задачах регрессии, т. е. приближения массива данных (Xi,yi) другими зависимостями у(х). Исключениерассмотрено в листинге 14.9.



Рис. 14.12. Линейная регрессия (листинг 14.7 или 14.8)
Для расчета линейной регрессии в MathCAD имеются два дублирующихдруг друга способа. Правила их применения представлены в листингах 14.7и 14.8. Результат обоих листингов получается одинаковым (рис. 14.12).
- line (х,у) - вектор из двух элементов (b,а) коэффициентов линейнойрегрессии b+а-х;
- intercept (х, у) - коэффициент ь линейной регрессии;- slope (х, у) - коэффициент а линейной регрессии;
 х - вектор действительных данных аргумента;
 у - вектор действительных данных значений того же размера.
Листинг 14.7. Линейная регрессия

Листинг 14.8. Другая форма записи линейной регрессии

В MathCAD имеется альтернативный алгоритм, реализующий не минимизацию суммы квадратов ошибок, а медиан-медианную линейную регрессиюдля расчета коэффициентов а и b (листинг 14.9).
- medfit(x,y) - вектор из двух элементов (b,а) коэффициентов линейноймедиан-медианной регрессии b+а-х;
 х, у - векторы действительных данных одинакового размера.
Листинг 14.9. Построение линейной регрессии двумя разными методами(продолжение листинга 14.7)

Различие результатов среднеквадратичной и медиан-медианной регрессиииллюстрируется рис. 14.13.


Рис. 14.13. Линейная регрессия по методу наименьших квадратови методу медиан (листинги 14.7 и 14.9)

14.2.2. Полиномиальная регрессия
В MathCAD реализована регрессия одним полиномом, отрезками нескольких полиномов, а также двумерная регрессия массива данных.
Полиномиальная регрессия
Полиномиальная регрессия означает приближение данных (xi,yi) полиномом k-й степени A(x)=a+b-x+c-x²+d-x³+.. .+h-x^k (рис. 14.14). При k=i полиномявляется прямой линией, при k=2 - параболой, при k=3 - кубической параболой и т. д. Как правило, на практике применяются k<5.

Примечание
Для построения регрессии полиномом k-й степени необходимо наличие покрайней мере (k+l) точек данных.

В MathCAD полиномиальная регрессия осуществляется комбинацией встроенной функции regress и полиномиальной интерполяции (см. разд. 14.1.2).
- regress (х, у, k) - вектор коэффициентов для построения полиномиальной регрессии данных;
- interp(s,x,y,t) - результат полиномиальной регрессии;
 s=regress(х,у,k);
 х - вектор действительных данных аргумента, элементы которогорасположены в порядке возрастания;
 у - вектор действительных данных значений того же размера;
 k - степень полинома регрессии (целое положительное число);
 t - значение аргумента полинома регрессии.
Для построения полиномиальной регрессии после функции regress вы обязаны использовать функцию interp.


Рис. 14.14. Регрессия полиномами разной степени (коллаж результатов листинга 14.10 для разных k)
Пример полиномиальной регрессии квадратичной -параболой приведен влистинге 14.10.
Листинг 14.10. Полиномиальная регрессия

Регрессия отрезками полиномов
Помимо приближения массива данных одним полиномом имеется возможность осуществить регрессию сшивкой отрезков (точнее говоря, участков,т. к. они имеют криволинейную форму) нескольких полиномов. Для этогоимеется встроенная функция loess, применение которой аналогично функции regress (листинг 14.11 и рис. 14.15).
- loess (x, у, span) - вектор коэффициентов для построения регрессииданных отрезками полиномов;
- interp(s,x,y,t) - результат полиномиальной регрессии;
 s=loess(x,y,span);
 х - вектор действительных данных аргумента, элементы которогорасположены в порядке возрастания;
 у - вектор действительных данных значений того же размера;
 span - параметр, определяющий размер отрезков полиномов (положительное число, хорошие результаты дает значение порядка span=0.75).
Параметр span задает степень сглаженности данных. При больших значениях span регрессия практически не отличается от регрессии одним полиномом (например, span=2 дает почти тот же результат, что и приближение точек параболой).
Листинг 14.11. Регрессия отрезками полиномов


Cовет
Регрессия одним полиномом эффективна, когда множество точек выглядит какполином, а регрессия отрезками полиномов оказывается полезной в противоположном случае.



Рис. 14.15. Регрессия отрезками полиномов(листинг 14.11)
Двумерная полиномиальная регрессия
По аналогии с одномерной полиномиальной регрессией и двумерной интерполяцией (см. разд. 14.1.5), MathCAD позволяет приблизить множествоточек Zi,j(xi,yj) поверхностью, которая определяется многомерной полиномиальной зависимостью. В качестве аргументов встроенных функций дляпостроения полиномиальной регрессии должны стоять в этом случае не векторы, а соответствующие матрицы.
- regress (x,z,k) - вектор коэффициентов для построения полиномиальной регрессии данных;
- loess (x,z, span) - вектор коэффициентов для построения регрессииданных отрезками полиномов;
- interp(s,x,z,v) - скалярная функция, аппроксимирующая данные выборки двумерного поля по координатам х и у кубическими сплайнами;
 s - вектор вторых производных, созданный одной из сопутствующихфункций loess ИЛИ regress;
 х - матрица размерности Nx2, определяющая пары значений аргумента (столбцы соответствуют меткам х и у);
 z - вектор действительных данных размерности N;
 span - параметр, определяющий размер отрезков полиномов;
 k - степень полинома регрессии (целое положительное число);
 v - вектор из двух элементов, содержащий значения аргументов х и у,для которых вычисляется интерполяция.
Для построения регрессии не предполагается никакого предварительного упорядочивания данных (как, например, для двумерной интерполяции, котораятребует их представления в виде матрицы NXN). В связи с этим данные представляются как вектор.
Двумерная полиномиальная регрессия иллюстрируется листингом 14.12 ирис. 14.16. Сравните стиль представления данных для двумерной регрессии спредставлением тех же данных для двумерной сплайн-интерполяции(см. листинг 14.6) и ее результаты с исходными данными (см. рис. 14.10) иих сплайн-интерполяцией (см. рис. 14.11).
Листинг 14.12. Двумерная полиномиальная регрессия


Примечание
Обратите внимание на знаки транспонирования в листинге. Они применены длякорректного представления аргументов (например, z, в качестве вектора, а нестроки).



Рис. 14.16. Двумерная полиномиальная регрессия(листинг 14.12)

14.2.3. Регрессия специального вида
Кроме рассмотренных, в MathCAD встроено еще несколько видов трехпа-раметрической регрессии. Их реализация несколько отличается от приведенных выше вариантов регрессии тем, что для них, помимо массива данных, требуется задать некоторые начальные значения коэффициентов а,b,с.Используйте соответствующий вид регрессии, если хорошо представляетесебе, какой зависимостью описывается ваш массив данных. Когда тип регрессии плохо отражает последовательность данных, то ее результат частобывает неудовлетворительным и даже сильно различающимся в зависимостиот выбора начальных значений. Каждая из функций выдает вектор уточненных параметров а, b, с.
expfit (x,y,g) - регрессия экспонентой f (x)=a-e^bx+c;
igsfit(x,y,g) - регрессия логистической функцией f (х)=а/(1+ь-е"^сх);
sinfit (x,y,g) - регрессия синусоидной f (x) =a-sin(x+b) +cj
pwfit(x,y,g) - регрессия степенной функцией f(x)=a-x^b+c;
logfit (x,y, g) - регрессия логарифмической функцией f (x)=a-in(x+b)+c;
infit(x,y) - регрессия двухпараметрической логарифмической функцией f (x)=a-ln(x)+b;
 x - вектор действительных данных аргумента;
 у - вектор действительных значений того же размера;
 g - вектор из трех элементов, задающий начальные значения а,b,с.

Примечание
Правильность выбора начальных значений можно оценить по результату регрессии - если функция, выданная MathCAD, хорошо приближает зависимостьу (х), значит они были подобраны удачно.

Пример расчета одного из видов трехпараметрической регрессии (экспоненциальной) приведен в листинге 14.13 и на рис. 14.17. В предпоследней строке листинга выведены в виде вектора вычисленные коэффициенты а,b,с,а в последней строке через эти коэффициенты определена искомая функция f(x).
Листинг 14.13. Экспоненциальная регрессия


Примечание
Многие задачи регрессии данных различными двухпараметрическими зависимостями у (х) можно свести к более надежной, с вычислительной точки зрения, линейной регрессии. Делается это с помощью соответствующей замены переменных.



Рис. 14.17. Экспоненциальная регрессия(листинг 14.13)

14.2.4. Регрессия общего вида
В MathCAD можно осуществить регрессию в виде линейной комбинацииCifi(x)+c₂f₂(x) + ..., где fi(x) - любые функции пользователя, ad - подлежащие определению коэффициенты. Кроме того, имеется путь проведениярегрессии более общего вида, когда комбинацию функций и искомых коэффициентов задает сам пользователь.
Приведем встроенные функции для регрессии общего вида и примеры ихиспользования (листинги 14.14 и 14.15), надеясь, что читатель при необходимости найдет более подробную информацию об этих специальных возможностях в справочной системе и Центре Ресурсов MathCAD.
- linfit(x,y, F) - вектор параметров линейной комбинации функцийпользователя, осуществляющей регрессию данных;
- genfit (x,y,g,G) - вектор параметров, реализующих регрессию данныхс помощью функций пользователя общего вида;
 х - вектор действительных данных аргумента, элементы которогорасположены в порядке возрастания;
 у - вектор действительных значений того же размера;
 F(X) - пользовательская векторная функция скалярного аргумента;
 g - вектор начальных значений параметров регрессии размерности N;
 G(x,o - векторная функция размерности N+I, составленная из функции пользователя и ее N частных производных по каждому из параметров с.
Листинг 14.14. Регрессия линейной комбинацией функций пользователя

Листинг 14.15. Регрессия общего вида

14.3.1. Встроенные функции для сглаживания
В MathCAD имеется несколько встроенных функций, реализующих различные алгоритмы сглаживания данных.
- medsmooth(y,b) - сглаживание алгоритмом "бегущих медиан";- ksmooth(x,y,b) - сглаживание на основе функции Гаусса;
- supsmooth(x,y) - локальное сглаживание адаптивным алгоритмом, основанное на анализе ближайших соседей каждой пары данных;
 х - вектор действительных данных аргумента (для supsmooth его элементы должны быть расположены в порядке возрастания);
 у - вектор действительных значений того же размера, что и х;
 b - ширина окна сглаживания.
Все функции имеют в качестве аргумента векторы, составленные из массиваданных, и выдают в качестве результата вектор сглаженных данных того жеразмера. Функция medsmooth предполагает, что данные расположены равномерно.

Примечание
Подробную информацию об алгоритмах, заложенных в функции сглаживания,вы найдете в справочной системе MathCAD в статье Smoothing (Сглаживание),находящейся в разделе Statistics (Статистика). Очень полезные сведенияо разных типах фильтрации можно отыскать в Центре Ресурсов.

Часто бывает полезным совместить сглаживание с последующей интерполяцией или регрессией. Соответствующий пример приведен в листинге 14.16 для функции supsmooth. Результат работы листинга показан на рис. 14.19(кружки обозначают исходные данные, крестики - сглаженные, пунктирнаякривая - результат сплайн-интерполяции). Сглаживание тех же данных припомощи "бегущих медиан" и функции Гаусса с разным значением шириныокна пропускания показаны на рис. 14.19 и 14.20, соответственно.


Рис. 14.18. Адаптивное сглаживание(листинг 14.16)
Рис. 14.19. Сглаживание "бегущими медианами"


Листинг 14.16. Сглаживание с последующей сплайн-интерполяцией

Рис. 14.20. Сглаживание при помощифункции ksmooth

14.3.2. Скользящее усреднение*
Помимо встроенных в MathCAD, существует несколько популярных алгоритмов сглаживания, на одном из которых хочется остановиться особо. Самый простой и очень эффективный метод - это скользящее усреднение.Его суть состоит в расчете для каждого значения аргумента среднего значения по соседним w данным. Число w называют окном скользящего усреднения; чем оно больше, тем больше данных участвуют в расчете среднего, темболее сглаженная кривая получается. На рис. 14.21 показан результат скользящего усреднения одних и тех же данных (кружки) с разным окном w=3(пунктир), w=5 (штрихованная кривая) и w=i5 (сплошная кривая). Видно, чтопри малых w сглаженные кривые практически повторяют ход измененияданных, а при больших w - отражают лишь закономерность их медленныхвариаций.


Рис. 14.21. Скользящее усреднение с разными w=3, 5,15 (листинг 14.17,коллаж трех графиков)
Чтобы реализовать в MathCAD скользящее усреднение, достаточно оченьпростой программы, приведенной в листинге 14.17. Она использует толькозначения у, оформленные в виде вектора, неявно предполагая, что они соответствуют значениям аргумента к, расположенным через одинаковые промежутки. Вектор х применялся лишь для построения графика результата(рис. 14.21).
Листинг 14.17. Сглаживание скользящим усреднением


Примечание
Приведенная программная реализация скользящего усреднения самая простая, но не самая лучшая. Возможно, вы обратили внимание, что все кривыескользящего среднего на рис. 14.21 слегка "обгоняют" исходные данные. Почему так происходит, понятно: согласно алгоритму, заложенному в последнююстроку листинга 14.17, скользящее среднее для каждой точки вычисляется путем усреднения значений предыдущих w точек. Чтобы результат скользящегоусреднения был более адекватным, лучше применить центрированный алгоритм расчета по w/2 предыдущим и w/2 последующим значениям. Он будетнемного сложнее, поскольку придется учитывать недостаток точек не тольков начале (как это сделано в программе с помощью функции условия if), но ив конце массива исходных данных.

14.3.3. Устранение тренда*
Еще одна типичная задача возникает, когда интерес исследований заключается не в анализе медленных (или низкочастотных) вариаций сигнала у(х)(для чего применяется сглаживание данных), а в анализе быстрых его изменений. Часто бывает, что быстрые (или высокочастотные) вариации накладываются определенным образом на медленные, которые обычно называюттрендом. Часто тренд имеет заранее предсказуемый вид, например линейный. Чтобы устранить тренд, можно предложить последовательность действий, реализованную в листинге 14.18.
1. Вычислить регрессию f(x), например линейную, исходя из априорнойинформации о тренде (предпоследняя строка листинга).
2. Вычесть из данных у(х) тренд f (х) (последняя строка листинга).
Листинг 14.18. Устранение тренда

На рис. 14.22 показаны исходные данные (кружками), выделенный с помощью регрессии линейный тренд (сплошной прямой линией) и результатустранения тренда (пунктир, соединяющий крестики).


Рис. 14.22. Устранение тренда (листинг 14.18)

14.3.4. Полосовая фильтрация*
В предыдущих разделах была рассмотрена фильтрация быстрых вариацийсигнала (сглаживание) и его медленных вариаций (снятие тренда). Иногдатребуется выделить среднемасштабную составляющую сигнала, уменьшивкак более быстрые, так и более медленные его компоненты. Одна из возможностей решения этой задачи связана с применением полосовой фильтрации на основе последовательного скользящего усреднения.


Рис. 14.23. Результат полосовой фильтрации(листинг 14.19)
Алгоритм полосовой фильтрации приведен в листинге 14.19, а результат егоприменения показан на рис. 14.23 сплошной кривой. Алгоритм реализуеттакую последовательность операций:
1. Приведение массива данных у к нулевому среднему значению путем еговычитания из каждого элемента у (третья и четвертая строки листинга).
2. Устранение из сигнала у высокочастотной составляющей, имеющее цельюполучить сглаженный сигнал middle, например, с помощью скользящегоусреднения с малым окном w (в листинге 14.19 w=3).
3. Выделение из сигнала middle низкочастотной составляющей slow, например, путем скользящего усреднения с большим окном w (в листинге 14.19 w=v), либо с помощью снятия тренда (см. разд. 14.3.3).
4. Вычесть из сигнала middle тренд slow (последняя строка листинга), темсамым выделяя среднемасштабную составляющую исходного сигнала у.
Листинг 14.19. Полосовая фильтрация

14.4.1. Преобразование Фурье
Математический смысл преобразования Фурье состоит в представлениисигнала у(х) в виде бесконечной суммы синусоид вида F(v)-sin(v-x). Функция F(V) называется преобразованием Фурье, или интегралом Фурье, илиФурье-спектром сигнала. Ее аргумент v имеет смысл частоты соответствующей составляющей сигнала. Обратное преобразование Фурье переводитспектр F(V) в исходный сигнал у (х). Согласно определению,
Преобразование Фурье действительных данных
Преобразование Фурье имеет огромное значение для различных математических приложений, и для него разработан очень эффективный алгоритм,называемый БПФ (быстрым преобразованием Фурье). Этот алгоритм реализован в нескольких встроенных функциях MathCAD, различающихся нормировками.
fft (у) - вектор прямого преобразования Фурье;
FFT (у) - вектор прямого преобразования Фурье в другой нормировке;
if ft (v) - вектор обратного преобразования Фурье;
IFFT (v) - вектор обратного преобразования Фурье в другой нормировке;
 у - вектор действительных данных, взятых через равные промежуткизначений аргумента;
 v - вектор действительных данных Фурье-спектра, взятых через равные промежутки значений частоты.
Аргумент прямого Фурье-преобразования, т. е. вектор у, должен иметь ровно 2"элементов (п - целое число). Результатом является вектор с l+2^n-1 элементами.И наоборот, аргумент обратного Фурье-преобразования должен иметь 1+2"¹элементов, а его результатом будет вектор из 2" элементов. Если число данныхне совпадает со степенью 2, то необходимо дополнить недостающие элементынулями.
Пример расчета Фурье-спектра для суммы трех синусоидальных сигналовразной амплитуды (показанных в виде сплошной кривой на рис. 14.24),приведен в листинге 14.20. Расчет проводится по N=128 точкам, причемпредполагается, что интервал дискретизации данных yi равен А. В предпоследней строке листинга применяется встроенная функция ifft, а в последней корректно определяются соответствующие значения частот О,±. Обратитевнимание, что результаты расчета представляются в виде модуля Фурье-спектра (рис. 14.25), поскольку сам спектр является комплексным. Оченьполезно сравнить полученные амплитуды и местоположение пиков спектрас определением синусоид в листинге 14.20.


Рис. 14.24. Исходныеданные и обратное преобразование Фурье(листинг 14.20)
Листинг 14.20. Быстрое преобразование Фурье



Рис. 14.25. Преобразование Фурье (листинг 14.20)
Результат обратного преобразования Фурье показан в виде кружков на томже рис. 14.24, что и исходные данные. Видно, что в рассматриваемом случаесигнал у(х) восстановлен с большой точностью, что характерно для плавного изменения сигнала.
Преобразование Фурье комплексных данных
Алгоритм быстрого преобразования Фурье для комплексных данных встроенв соответствующие функции, в имя которых входит литера "с".
- cfft (у) - вектор прямого комплексного преобразования Фурье;
- CFFT (у) - вектор прямого комплексного преобразования Фурье в другойнормировке;
- icfft (у) - вектор обратного комплексного преобразования Фурье;
- ICFFT (v) - вектор обратного комплексного преобразования Фурье в другой нормировке;
 у - вектор данных, взятых через равные промежутки значений аргумента;
 v - вектор данных Фурье-спектра, взятых через равные промежуткизначений частоты.
Функции действительного преобразования Фурье используют тот факт, чтов случае действительных данных спектр получается симметричным относительно нуля, и выводят только его половину (см. выше разд. "ПреобразованиеФурье действительных данных" этой главы). Поэтому, в частности, по 128действительным данным получалось всего 65 точек спектра Фурье. Если ктем же данным применить функцию комплексного преобразования Фурье(рис. 14.26), то получится вектор из 128 элементов. Сравнивая рис. 14.25и 14.26, можно уяснить соответствие между результатами действительного икомплексного Фурье-преобразования.


Рис. 14.26. Комплексное преобразование Фурье (продолжение листинга 14.20)
Двумерное преобразование Фурье
В MathCAD имеется возможность применять встроенные функции комплексного преобразования Фурье не только к одномерным, но и к двумерным массивам, т. е. матрицам. Соответствующий пример приведен в листинге 14.21 и на рис. 14.27 в виде графика линий уровня исходных данных ирассчитанного Фурье-спектра.
Листинг 14.21. Двумерное преобразование Фурье



Рис. 14.27. Данные (слева) и их Фурье-спектр (справа) (листинг 14.21)

14.4.2. Вейвлетное преобразование
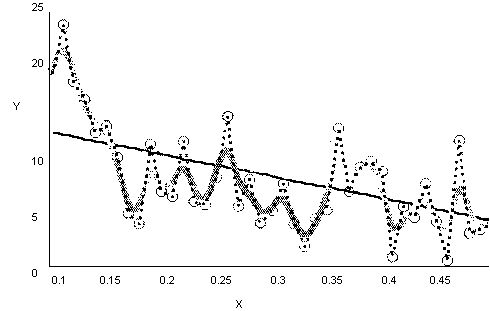
В последнее время возрос интерес к другим интегральным преобразованиям,в частности вейвлетному (или дискретному волновому) преобразованию. Оноприменяется, главным образом, для анализа нестационарных сигналов и длямногих задач подобного рода оказывается более эффективным, чем преобразование Фурье. Основным отличием вейвлетного преобразования являетсяразложение данных не по синусоидам (как для преобразования Фурье), а подругим функциям, называемым вейвлетобразующими. Вейвлетобразующиефункции, в противоположность бесконечно осциллирующим синусоидам,локализованы в некоторой ограниченной области своего аргумента, а вдалиот нее равны нулю или ничтожно малы. Пример такой функции, называемой "мексиканской шляпой", показан на рис. 14.28.


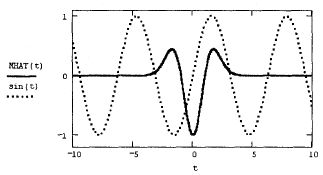
Рис. 14.28. Сравнение синусоиды и вейвлетобразующей функции
Из-за своего математического смысла вейвлет-спектр имеет не один аргумент, а два. Помимо частоты, вторым аргументом ь является место локализации вейвлетобразующей функции. Поэтому ь имеет ту же размерность,что и х.
Встроенная функция вейвлет-преобразования
MathCAD имеет одну встроенную функцию для расчета вейвлет-преобразования на основе вейвлетобразующей функции Даубечи.
- wave (у) - вектор прямого вейвлет-преобразования;- iwave (v) - вектор обратного вейвлет-преобразования;
 у - вектор данных, взятых через равные промежутки значений аргумента;
 v - вектор данных вейвлет-спектра.
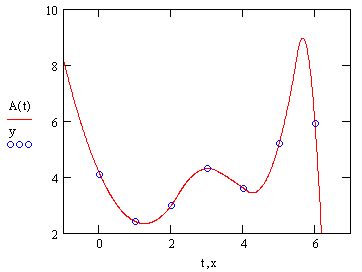
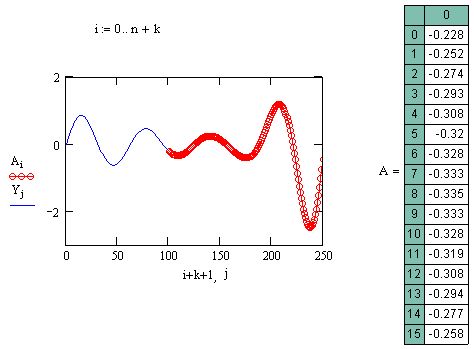
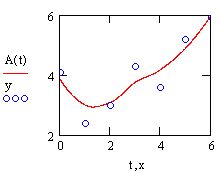
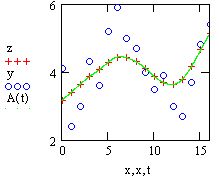
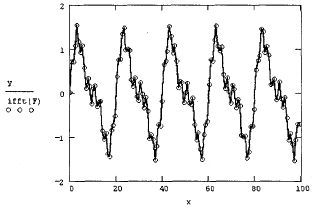
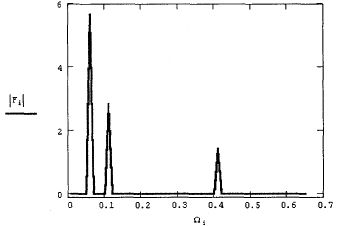
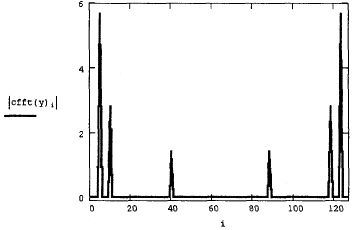
Аргумент функции вейвлет-преобразования, т. е. вектор у, должен так же,как и в преобразовании Фурье, иметь ровно 2^П элементов (п - целое число).Результатом функции wave является вектор, скомпонованный из несколькихкоэффициентов с двухпараметрического вейвлет-спектра. Использованиефункции wave объясняется на примере анализа суммы двух синусоид в листинге 14.22, а три семейства коэффициентов вычисленного вейвлет-спектра показаны на рис. 14.29
Листинг 14.22. Поиск вейвлет-спектра Даубечи



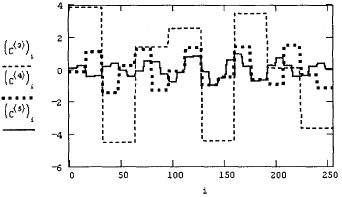
Рис. 14.29. Вейвлет-спектр на основе функции Даубечи (листинг 14.22)
Программирование других вейвлет-преобразований*
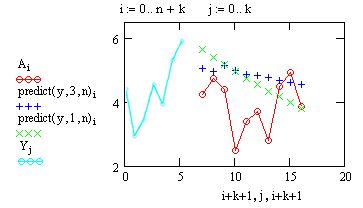
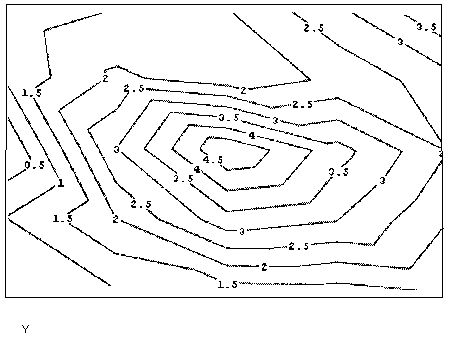
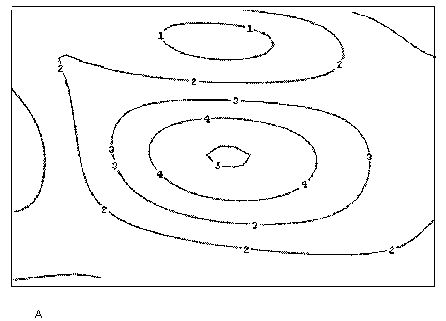
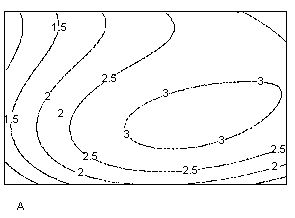
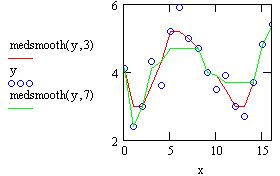
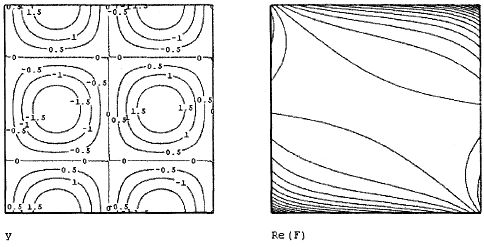
Наряду со встроенной функцией wave, возможно программирование своихалгоритмов расчета вейвлет-спектров. Оно сводится к аккуратному расчетусоответствующих семейств интегралов. Один из примеров такой программыприведен в листинге 14.23, а ее результат на рис. 14.30. Анализу подвергается та же функция, составленная из суммы двух синусов, а график двухпара-метрического спектра с(а,b) выведен в виде привычных для вейвлет-анализа линий уровня на плоскости (а,b).
Листинг 14.23. Поиск вейвлет-спектра на основе "мексеканской шляпы"


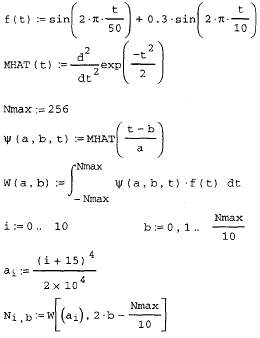
Примечание
Программа листинга очень проста, но исключительно далека от хорошейв смысле быстро действия. Каждый интеграл вычисляется независимо, безиспользования методов ускорения, типа применяемых в алгоритме БПФ.



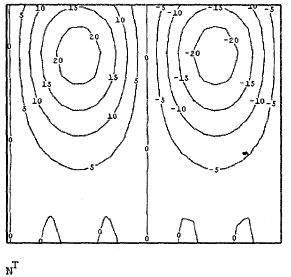
Рис. 14.30. Вейвлет-спектр на основе "мексиканской шляпы" (листинг 14.23)

Глава 13 Содержание Глава 15