Программа Excel
может быть использована для проведения
сравнительно несложных математических расчетов.
Для проведения вычислений по сложным
математическим зависимостям разработаны
специальные пакеты, например, MatLab, MatCAD. Тем не
менее, многие вычисления Excel вполне доступны.
7.1. Функции
Математические
вычисления обычно связаны с использованием функций.
Программа Excel имеет богатую библиотеку функций,
которая структурирована по категориям. Когда
необходимо вставить функцию в формулу лучше
использовать Мастер функций.
Запустите Excel,
сохраните новую книгу под именем Функции.xls.
Поместите курсор на какую-нибудь ячейку и
выполните вставку функции. Сделать это можно
тремя способами: командой Вставка/Функция,
кнопкой Вставка функции  на панели Стандартная,
нажатием клавиш Shift+F3. При этом откроется окно Мастер
функций, которое показано на рис. 7.1. на панели Стандартная,
нажатием клавиш Shift+F3. При этом откроется окно Мастер
функций, которое показано на рис. 7.1.
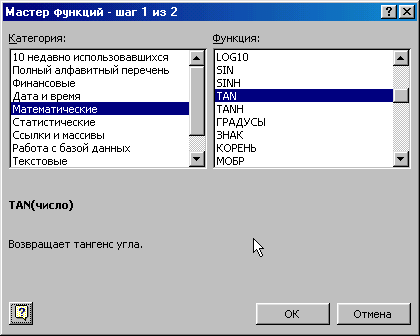 |
Рис. 7.1. Мастер функций |
В левом
списке перечислены категории функций.
Щелкните в нем, например, по строке Математические.
Справа в списке Функция появится список
математических функций. Щелкните в нем, например,
по функции TAN. Ниже будет показан синтаксис
функций о указан тип возвращаемого значения.
Из пояснений следует, что выбранная функция есть
тангенс числа, она имеет один аргумент.
Ниже в табл. 7.1 приведен
список некоторых наиболее распространенных
математических операций и функций.
Таблица 7.1.
Некоторые функции Excel |
| Операция/функция |
Примечание |
| - |
вычитание; |
| * |
умножение; |
| / |
деление; |
| - |
вычитание |
| + |
сложение |
| ^ |
возведение в степень |
| ABS(число) |
абсолютная величина; |
| ACOS(число) |
арккосинус; |
| ASIN(число) |
арксинус; |
| ATAN(число) |
арктангенс; |
| COS(число) |
косинус; |
| COSH(число) |
косинус гиперболический; |
| EXP(число) |
экспонента; |
| LN(число) |
натуральный логарифм; |
| LOG(число;
основание) |
логарифм числа с заданным
основанием; |
| LOG10(число) |
десятичный логарифм; |
| SIN(число) |
синус; |
| SINH(число) |
синус гиперболический; |
| TAN(число) |
тангенс; |
| TANH(число) |
тангенс гиперболический; |
| КОРЕНЬ(число) |
квадратный корень; |
| ОТБР(число) |
целое, полученное
отбрасыванием дробной части; |
| ПИ() |
число 3,14159265358979 |
| ПРОИЗВЕД(число1;число2;…;
числоN) |
произведение заданного
числа аргументов; |
| РАДИАНЫ(число) |
преобразует градусы в
радианы; |
| РИМСКОЕ(число) |
преобразует арабское
число в римское; |
| СТЕПЕНЬ(число;
степень) |
возводит число в степень; |
| СУММ(число1;
число2; …; числоN); |
сумма N чисел; |
| ФАКТ(число) |
факторил 1*2*3*…*число; |
| ЦЕЛОЕ(число) |
округление |
|
Формулой
называется выражение, которое введено в ячейку.
Формула всегда начинается с символа “=”. Формула
может относиться к различным типам. Если
результатом вычисления является число, то
формула называется арифметической. В состав
арифметической формулы могут входить числа,
адреса ячеек (переменные), знаки операций,
функции и круглые скобки. Последние служат для
указания порядка выполнения операций.
В табл. 7.2. приведены примеры
Excel-формул.
Функция |
Комментарий |
=3 + 6
=F7 + 7,88
=КОРЕНЬ(2/H5)
=КОРЕНЬ(ABS(LOG10(G2)+EXP(7,67*D2))) |
Сумма 3 и 6; Сумма числа из ячейки F7 и числа 7,88;
Квадратный корень из числа 2,
деленного на число из ячейки H5;
Квадратный корень из абсолютной
величины суммы десятичного логарифма числа из
ячейки G2 и экспоненты от произведения числа 7,67 и
числа из ячейки D2; |
Типичной
расчетной задачей является табулирование
математических функций. Суть ее состоит в
построении таблицы значений функции.
Рассмотрим задачу.
Построить таблицу значений функции
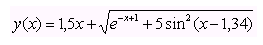
для x = 0; 0,1; 0,2; …; 1,5.
Заметим, что ряд аргументов
представляет собой последовательность из 16-ти
чисел с одинаковым расстоянием 0,1 между ними. Это
свойство можно использовать для быстрого ввода
чисел этого ряда. Введите в ячейку А3 число 0, в А4
– число 0,1. Выделите эти ячейки. У ячейки А4
ухватите маркер автозаполнения и протяните его
до ячейки А18. Весь ряд заполнится нужными
числами, т. е. числами от 0 до 1,5 с шагом 0,1.
Теперь введите формулу для
функции в ячейку B3. Щелкните по ней. Поскольку
формула будет длинной, то вводите ее не в ячейку,
а в специальную строку ввода, которая находится
сразу над таблицей (рис. 7.1).
 |
Рис. 7.1.
Строка ввода с формулой |
Формула
имеет вид
=1,5*A3+КОРЕНЬ(EXP(-A3+1)+5*SIN(A3-1,34)^2)
После ввода закройте ячейку
клавишей Enter. Найдите маркер автоподбора ячейки B3
и протяните его до ячейки B18. Расчет закончен.
Для
повышения наглядности данных, заложенных в
сформированную таблицу, введите заголовок и
подписи к столбцам. Отформатируйте числа первого
столбца, указав один знак в дробной части. Для
чисел второго столбцы назначьте в дробную часть 3
знака. Отрегулируйте ширину столбцов и
расположите числа по середине ячеек. В
окончательном виде таблица значений аргумента x
и соответствующих им значений функции y(x)
показана на рис. 7.2.
Для большей наглядности
постройте график значений этой функции. Щелкните
по ячейке вне таблицы Запустите Мастер
диаграмм. В окне первого шага щелкните по
закладке Нестандартные, затем по строке Гладкие
графики. В окне второго шага укажите
расположение рядов в столбцах. Щелкните на
кнопке строки Диапазон и выделите
вычисленные
значения функции (ячейку заголовка не выделяйте).
Снова щелкните по кнопке диапазона. Окно
распахнется. Щелкните на закладке Ряд. Теперь
щелкните по кнопке строки Подписи оси X: и
выделите ряд значений аргумента (в столбце x).
На третьем шаге на закладке Заголовки
внесите название График функции. На закладке Линии
сетки поставьте галочки опций основные
линии по обеим осям. На закладке Легенда
снимите галочку опции Добавить легенду.
Закройте Мастер диаграмм. Отрегулируйте шрифты и
положение графика на подложке. Диаграмма примет
вид, показанный на рис. 7.3. |
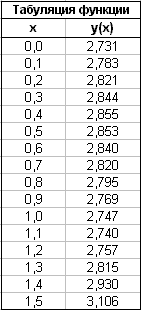 |
Рис. 7.2.
Табулирование
функции |
|
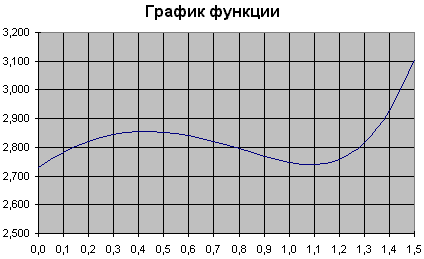 |
Рис. 7.3.
График функции y(x) |
| Выполните
табуляцию одной из функций (табл. 7.1) по варианту и
постройте ее график. Номер варианта назначает
преподаватель. Вставьте таблицу и график в свой
отчет. |
|
Таблица 7.1
| № |
Функция |
Аргумент:
начало, конец, шаг |
1. |
y=Exp(-x3) (1,6 x-1,7) |
x = 0; 1,2; 0,1 |
2. |
y=2x Sin (5 x2) |
x = 0.2; 1,4; 0,1 |
3. |
y=x2 Cos (8 x2 –0,5) |
x = -0.2; 1,0; 0,1 |
4. |
y=(2 Cos2 (4x –1) +
Sin2 (3x+1)) 1/2 |
x = 0; 1,2; 0,1 |
5. |
y=2 (x-0,25) 3 / (x+0,5) |
x = -0,2; 1,2; 0,1 |
6. |
y=Ln(2x +1+ 3 Sin2 (x)) |
x = -1,4; 0,4; 0,1 |
7. |
y=Ln(x2 + Exp(-x)) |
x = -0,2; 1,6; 0,1 |
8. |
y=Ln(x+ 2 +5 Sin(x)) |
x = 0; 2; 0,1 |
|


