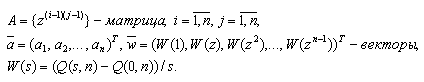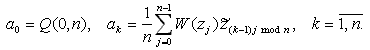ЧИСЛЕННЫЙ  МЕТОД  ОПРЕДЕЛЕНИЯ   ПЕРЕДАТОЧНОЙ  ФУНКЦИИ ДИНАМИЧЕСКОГО   ОБЪЕКТА  В  ИНТЕЛЛЕКТУАЛЬНОЙ  СРЕДЕ

Коднянко В.А., канд.техн.наук, доцент
(Красноярский государственный технический университет, Россия, Красноярск)

           При моделировании, расчете и исследовании динамики сложных технических объектов в интеллектуальных средах исходную математическую модель удобно представлять в виде иерархической структуры взаимосвязных моделей отдельных блоков, описанных языком представления знаний предметной области [1]. Для расчета критериев динамического качества чаще используют метод малых отклонений, в соответствии с которым исходную математическую модель трансформируют при помощи преобразования Лапласа в соответствующую модель относительно изображений малых отклонений нестационарных функций от равновесного состояния объекта [2]. Обычно коэффициентами при изображениях являются полиномы параметра Лапласа - комплексной переменной s. Однако для ряда объектов, например газостатических опор, в которых изображения связаны сложными интегро-дифференциальными зависимостями, такое представление удается получить только для частных случаев [3]. Достаточная для практики точность представления коэффициентов может быть получена с помощью трансцендентных функций либо численными методами [4]. Во всех случаях передаточную функцию (ПФ) объекта можно определить в виде отношения полиномов переменной s предлагаемым численным методом.
          Для определения ПФ линеаризованную модель каждого блока, включая сам объект, представим лингвистической процедурной моделью g_i (X_i, Y_i, L_i, D_i, G_i, M_i, s), где g_i - ее имя, X_i - множество статических параметров, Y_i = (y_i1, y_i2, …, y_in) - множество глобальных изображений, L_i = (l_i1, l_i2,…, l_im) - множество локальных изображений, D_i = (d_i1, d_i2,…, d_it) - множество дополнительных изображений, G_i = (g_i1, g_i2, …, g_ik) - множество ссылок на модели внутренних блоков, реализующих их фактическое представление внутри модели g_i, M_i - динамическая матрица связей глобальных, локальных и дополнительных изображений модели. Всякая i-тая связь модели имеет вид

Связь представлена отдельной строкой матрицы.
          Обобщенная модель объекта составит множество G = (g₁, g₂, …, g_u), где u - число моделей. Метод предполагает, что к началу формирования ПФ значения параметров из множеств X₁, X₂, …, X_u известны, а также известны номера r, v входного и выходного глобальных изображений головной модели, находящейся в корне дерева иерархии моделей объекта. Его схема показана на рис. 1.

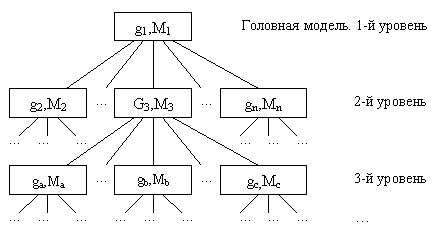
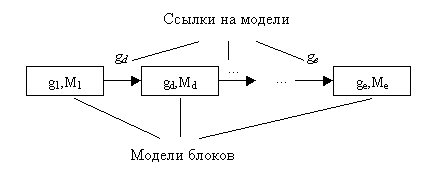
Рис. 1. Дерево иерархии динамического объекта

          Опишем метод вычисления ПФ для одного значения переменной s. В начале создается матрица М₁ связей головной модели g₁, количество строк которой равно количеству глобальных и локальных изображений, а количество столбцов равно количеству явных связей. Элементы матрицы равны значениям коэффициентов при изображениях для заданного значения s. Далее призводится спуск от корневой модели g₁ во все подчиненные ей модели g₁₁, g₁₂, …, g_1n, подключенные при помощи ссылок g₁₁, g₁₂, …, g_1n. Аналогичным образом производится начальное формирование матриц этих моделей, затем производится спуск на следующий уровень и т. д. Рекурсивный спуск выполняется до тех пор, пока не будут достигнуты концевые вершины на всех ветвях дерева. Схема спуска от корня дерева к концевой вершине отдельной ветви показана на рис. 2.

Рис. 2. Схема спуска по отдельной ветви иерархического дерева

           В каждой паре соседних моделей ветви назовем левую модель А-моделью (подключающая модель), правую - Б-моделью (подключаемая модель). Для моделей, находящихся в концевых вершинах ветвей, не существует Б-моделей, а начальное и конечное состояния матриц совпадают, т. к. в теле этих моделей нет ссылок на подключаемые модели блоков. Для корневой модели не существует А-модели.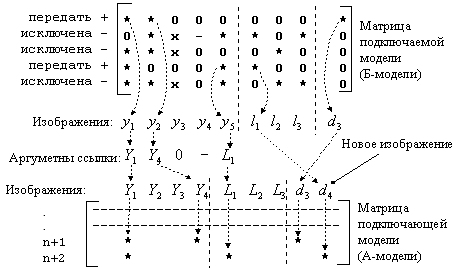
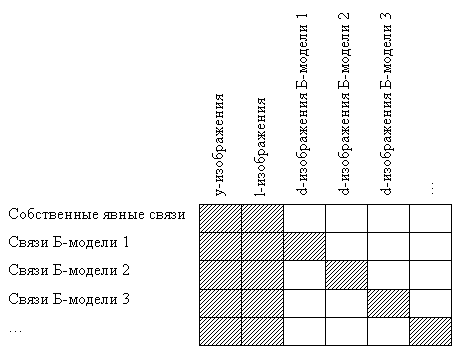
          Дальнейший расчет ПФ связан с обратным ходом от концевых вершин ветвей к корню иерархического дерева с целью окончательного формирования матрицы M₁ головной модели объекта.
          Структура связей Б-модели определяется ее содержанием и ссылкой. Последняя может потребовать исключения некоторых изображений, следствием чего может стать отключение ряда связей. Ссылка может содержать прямое указание на отключение определенных связей. По этой причине одна и та же формальная модель при различном ее представлении ссылками может порождать фактические модели с различной конфигурацией соответствующих матриц.
          Процесс восхождения начинается с моделей концевых вершин. Сначала в Б-модели производится исключение l-изображений. Исключению подлежат только те изображения, которые имеют не зависящие от s и отличные от нуля коэффициенты. Соблюдение этого условия гарантирует правильное вычисление значений числителя и знаменателя ПФ (несоблюдение условия исключает возможность раздельного вычисления этих компонент в рамках предлагаемого метода). Поскольку процесс является численным, то тип коэффицента при исключаемом изображении следует контролировать закрепленным за ним параметром-признаком. Возможны ситуации, когда некоторые l-изображения исключить не удастся из-за недостатка связей, либо отсутствия коэффициентов, удовлетворяющих упомянутому условию. В таких случаях в А-модели создается новое d-изображение, а в матрице - соответствующий ему столбец. Затем неисключенные связи Б-модели передается в А-модель с целью пополнения ее матрицы, после чего матрица Б-модели может быть разрушена. Процессом передачи управляет ссылка, подключавшая Б-модель. Таким способом производится последовательная передача в А-модель неисключенных связей из всех Б-моделей. В результате матрица А-модели оказывается полностью сформированной. Если А-модель активизирована ссылкой, то она становится Б-моделью и передает далее неисключенные связи в свою А-модель и т. д. На рис. 3 приведен пример схемы передачи связей.

Рис. 3. Пример схемы передачи связей из Б-модели в А-модель

          Б-модель имеет изображения: y₁, y₂, y₃, y₄, y₅ - глобальные, l₁, l₂, l₃ - локальные, d₃ - дополнительное (наличие последнего указывает на то, что оно получено ранее при передаче в нее, как в А-модель, связей из какой-либо ее Б-модели). В исходном состоянии А-модель содержит изображения: Y₁, Y₂, Y₃, Y₄ - глобальные, L₁, L₂, L₃ - локальные. Ссылка, которая подключает Б-модель, имеет аргументы: Y₂, Y₄, 0, - . Первый параметр указывает на то, что роль y₁ Б-модели играет изображение Y₂ из А-модели, а Y₄ играет роль y₂. Третий параметр ссылки ("0") означает, что в матрице Б-модели все ненулевые элементы третьего столбца следует положить равными нулю (на схеме они обозначены символом "х"). Четвертый параметр ("-") требует исключения из Б-модели строк, содержащих ненулевые элементы в четвертом столбце (на схеме элемент обозначен символом "-"). Третья строка использована для исключения изображения l₂, пятая - для исключения l₃. Вторая строка исключена по указанию ссылки. Первая строка непригодна для исключения l₁, а четвертую строку не удалось использовать для этой операции из-за невыполнения упомянутого выше условия. Эти строки подлежат передаче (на схеме они помечены символом "+"). К этому моменту матрица-приемник имеет n явных связей. Передаваемые связи следует разместить в двух последующих ее строках. Передача коэффициентов глобальных изображений Б-модели регулируется ссылкой, на основании которой, элементы матрицы при y₁, y₂, y₅ должны быть трансформированы в элементы при Y₂, Y₄, L₁ матрицы-приемника, соответственно. Изображение d₃ передается в неизменном виде, для неисключенного изображения l₁ в А-модели нужно создать новое d-изображение d₄. Схема передачи коэффициентов (помечены символом "*") показана стрелками. После сборки матрица А-модели примет вид, показанный на рис. 4.

Рис. 4. Структура собранной матрицы А-модели

          Заштрихованные клетки матрицы содержат ненулевые элементы или нули, незаштрихованные - только нули.
          Восхождение производится до головной А-модели g₁, где будет окончательно сформирована ее матрица М₁. Для корректной модели число строк М₁ должно быть на единицу меньше числа столбцов (М₁ является аналогом расширенной матрицы системы линейных уравнений).
          Далее нужно создать две квадратные матрицы М_Q и M_P. Первая получается из М₁ вычеркиванием r-столбца. Вторая - из М_Q заменой v-столбца, унаследованного из М₁, на r-столбец М_1. Теперь следует вычислить определители Q(s) = det(М_Q) - знаменатель ПФ, P(s) = (-1)^r+1 det(M_P) - числитель ПФ и Ф(s) = y_v /y_r = P(s)/Q(s) - значение ПФ для заданного s.
          В этом виде описанный метод пригоден для расчета ПФ объекта частотными методами теории систем автоматического регулирования (САР).
          На практике часто необходимо выполнить расчет устойчивости объекта при помощи корневых критериев САР. Для этого используется характеристический полином, который совпадает со знаменателем ПФ для моделей с полиномиальными коэффициентами при изображениях, либо представляет его приближенно - в остальных случаях. Для его определения представим знаменатель ПФ в виде полинома

где a₀, a₁, …, a_n - неизвестные коэффициенты, n - неизвестный порядок.
          Положим z = Exp (2i/n), где i = (-1)^1/2. Последовательно подставив в полином s = 0, 1, z, z², …, z^n-1 и вычислив Q описанным методом, получим систему линейных уравнений относительно неизвестных коэффициентов, которая имеет вид:

где

Матрица А является матрицей Вандермонда [5]. Она имеет обратную матрицу А^-1

Символом ~ обозначена операция комплексного сопряжения.
          Выполнив преобразования, найдем неизвестные коэффициенты по формулам:

           Если коэфиициенты связей всех моделей объекта имеют полиномиальный вид, то значение n определяется один раз. Если модели содержат трансцендентные коэффициенты либо они получены численно, то порядок аппроксимирующего характеристического полинома может изменяться в зависимости от требуемой точности аппроксимации. Найти порядок можно, например, итерационным методом, начиная с n = 0, последовательным увеличичением его значения до тех пор, пока не выполнится условие сходимости. В качестве критерия можно использовать, например, следующее условие:

где e - относительная погрешность аппроксимации. При необходимости аналогично может быть определен числитель ПФ.
          Метод реализован в интеллектуальной исследовательской среде СИГО [6]. Проведенные расчеты потвердили его работоспособность.

СПИСОК ЛИТЕРАТУРЫ

1. Искусственный интеллект. - В 3-х кн. Кн. 2. Модели и методы: Справочник/ Под ред. Д. А. Поспелова - М.: "Радио и связь", 1990, 304 с.
2. Справочное пособие по теории систем автоматического регулирования и управления. Под.общ.ред. Е.А.Санковского. Мн. "Вышэйш.школа", 1973, 584 с.
3. Коднянко В. А., Шатохин С. Н. Радиальный газостатический подшипник с активным регулированием расхода газа эластичными компенсаторами. "Машиноведение", 1981, № 5, с.с. 107 - 112.
4. Коднянко В. А. Преимущества численного решения линеаризованного нестационарного уравнения Рейнольдса при расчете динамики газостатических опор. "Проблемы машиностроения и надежности машин", 2000 (в печати).
5. Беллман Р. Введение в теорию матриц. М."Наука", 1969, 368 с.
6. Коднянко В. А. СИГО - среда моделирования, расчета и исследования конструкций с газостатичскими опорами. Труды Четвертого Международного конгресса "Конструкторско-технологическая информатика - 2000", Станкин, 2000, Том 1, с. с. 277 - 279.