Структуры алгоритмов

Существует несколько типов алгоритмов: линейные, разветвляющие, циклические.

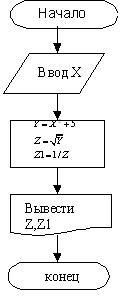
Линейный алгоритм

Имеет простую линейную структуру, в которой все шаги выполняются друг за другом один раз в порядке их следования.

Например: Дано X.  Вычислить  Z = У1/2  и  Z1 = 1 /Z ,
                        если Y = X2 + 5.

Словесное описание линейного алгоритма имеет следующий вид:

  1. Ввести X
  2. Вычислить Y = X2 + 5
  3. Вычислить Z = Y1/2
  4. Вычислить Z1 = 1/Z
  5. Вывести Z1, Z
  6. Конец.
Рис. 1.1. Графическое изображение линейного алгоритма

Разветвляющийся алгоритм

Разветвляющийся алгоритм - последовательность выполнения шагов алгоритма изменяется в зависимости от некоторых условий. Осуществляется выбор одного из двух/нескольких возможных вариантов. Словесно эта конструкция записывается так:

ЕСЛИ условие справедливо, ТО выполнить действия 1,

ИНАЧЕ выполнить действия 2.

Разветвляющийся алгоритм содержит блок проверки некоторого условия, и в зависимости от результата проверки выполняется та или иная последовательность шагов (действий).

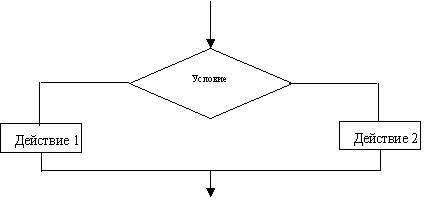
Если есть «действия 1» и «действия 2», то говорят о полной альтернативе(рис.1.2).

Рис. 1.2. Полная альтернатива

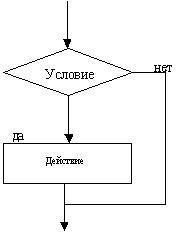
Если же в качестве «действия 2» имеет место формулировка «перейти к п. N», то такая форма записи называется неполной альтернативой (рис. 1.3).

Рис. 1.3. Неполная альтернатива

Например, составить алгоритм для вычисления функции:

     (X+1,Y>0,)
Z =

     (X+Y, Y<0.)

Словесное описание разветвленного алгоритма имеет следующий вид:

  1. Ввести X
  2. Если Y > 0, то Z = X + 1
  3. Если Y <0
    Вывести Z = X + Y
  4. Конец.
Рис. 1.4. Графическое изображение разветвленного алгоритма

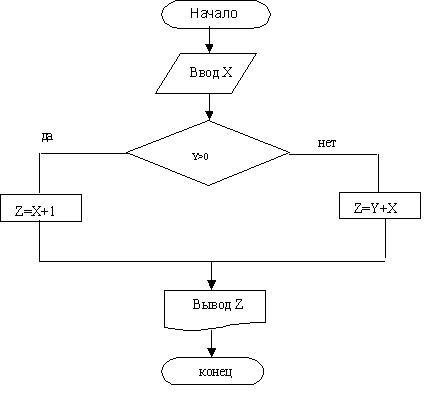
Условие - это логическое выражение, которое может принимать два значения -«да», если условие верно, и «нет», если условие не выполняется. На рис. 1.5 приведена схема алгоритма Евклида (вычисление НОД), словесная запись которого была приведена выше.


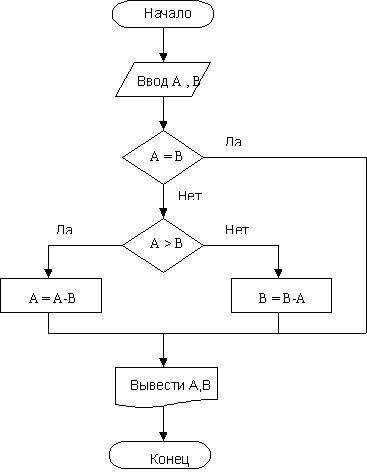
Рис. 1.5. Схема алгоритма Евклида - определение наибольшего общего делителя

Циклический алгоритм

Для обозначения многократно повторяющихся действий используются специальные циклические структуры. Такая структура содержит условие, которое необходимо для определения количества повторений для некоторой последовательности действий.

Основной блок цикла - тело цикла - производит требуемые вычисления. Вспомогательные блоки цикла организуют циклический процесс: устанавливают начальное значение и новые значения данных, проверяют условие окончания циклического процесса.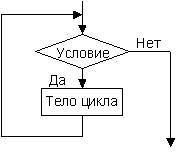

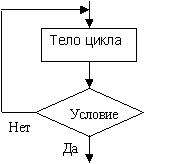
Рис. 1.6. Цикл с предусловием. Тело цикла может не выполняться ни одного раза

Циклический алгоритм позволяет компактно описать большое число одинаковых вычислений над разными данными для получения необходимого результата. Различают циклические структуры с предварительным условием (рис. 1.6) - циклы с предусловием и циклические структуры с последующим условием (рис. 1.7) -циклы с постусловием.

Рис. 1.7. Цикл с постусловием. Тело цикла выполнится хотя бы один раз

Для организации любого цикла необходимо следующее:
1. Задать перед началом цикла начальные значения параметров цикла.
2. Изменять параметры цикла перед каждым новым повторением цикла.
3. Проверять условие повторения или окончания цикла.
4. Переходить к началу цикла, если он не закончен, или выходить из цикла.

По способу определения числа повторений различают также циклы с неизвестным числом повторений и циклы с явно заданным числом повторений. Примером цикла с неизвестным числом повторений является итерационный цикл. Выход из итерационного цикла осуществляется не после того, как цикл повторится заданное число раз, а при выполнении условия более общего характера, связанного с проверкой значения монотонно изменяющейся в цикле величины. Часто эта величина характеризует точность, достигнутую на очередном шаге итерационного процесса, реализуемого алгоритмом.