|
НиТ.
Раритетные издания:
Физики продолжают шутить
|
Ключ к системе ключейДлинное письмо в редакцию
Ранее было высказано мнение, что система дверных ключей в нашем институте сложнее, чем теория поля. Это явное извращение фактов, и чтобы его опровергнуть, в настоящем сообщении мы излагаем упрощенную теоретическую схему, на основе которой создавалась эта система. Начнем с определений. Ключ состоит из стержня, на котором укреплены штифты. Замок состоит из щели с отверстиями, расположенными соответственно позициям штифтов на стержне ключа. Кроме того, в замке имеется система рычажков, находящихся позади отверстий (см. рисунок). Введем теперь следующие три аксиомы:
Пусть штифты, отверстия и рычажки описываются значением 1 переменных aj, bj, и сj, соответственно. Индекс j – номер позиции. Антиштифты, антиотверстия и антирычажки соответствуют значению 0 тех же переменных. Определим теперь матричное умножение следующим способом:
где символическое произведение abc = a, если одновременно а ≤ b и а ≥ с, в противном случае abc = 1 – α. Отсюда следует, что если (a1 а2...аk) есть собственный вектор оператора
то ключ может отпереть замок. Используя этот формализм, легко найти полное число ключей, которые открывают данный замок
а число замков, которые могут быть открыты данным ключом (α), равно
При получении этих выражений учитывался тот факт, что замок В уравнениях (2) и (3) k есть сумма коэффициентов Клебша – Гордана, равная единице. Развитый выше формализм позволил решить следующую задачу. Пусть некто хочет пройти из некоторой комнаты A через несколько дверей в произвольную комнату B. Число ключей, необходимое для этого, максимизировалось при произвольном выборе комнат A и B. (Проблема минимизации не решалась, поскольку ее решение тривиально – одинаковые замки.) Затем сотрудники института были разбиты на ряд подгрупп, и система ключей строилась таким образом, чтобы одновременно выполнялись два условия: 1) ни одна подгруппа не в состоянии открыть все те замки, которые могут быть открыты любой другой подгруппой; 2) трансформационные свойства групп соответствуют возможности одалживания ключей. Создатели системы ключей надеялись, что она является единственно возможной и полной, и до известной степени это справедливо. Однако оказалось, что ключи, которые не должны были бы открывать некоторые двери, открывают их, если их вставлять в замок не до конца. Например, ключ (11111) может открыть замок На отмычки настоящее исследование не распространяется. Автор выражает благодарность сотрудникам, работающим в разных группах, за горячее обсуждение затронутых проблем.
Текст издания: Физики продолжают шутить. Сборник переводов. Дата публикации: 17 августа 2000 года |
|
Электронная версия: © «НиТ. Раритетные издания», 1998 | |
Раритетные издания • Аналитический центр • Нобелевские лауреаты • Конкурсы • Cовместные проекты • Текущие публикации • Дискуссии и диспуты • Издания НиТ | |
| © НиТ, 1997...2001 | nit@n-t.org |
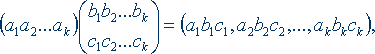
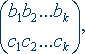
 в n = 5 различных положениях. Число n было названо странностью системы ключ – замок. Экспериментальными исследованиями было найдено, что наша система ключей является весьма странной. Однако этот недостаток можно исправить, если потребовать для последней позиции соблюдения равенств аk = bk = сk = 1. Будем надеяться, что при ближайшем пересмотре системы ключей в нее будет внесено это исправление.
в n = 5 различных положениях. Число n было названо странностью системы ключ – замок. Экспериментальными исследованиями было найдено, что наша система ключей является весьма странной. Однако этот недостаток можно исправить, если потребовать для последней позиции соблюдения равенств аk = bk = сk = 1. Будем надеяться, что при ближайшем пересмотре системы ключей в нее будет внесено это исправление.