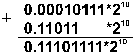
| [ следующий ] [ начало главы ] [ предыдущий ] | [ содержание ] |
К началу выполнения арифметического действия операнды операции помещаются в соответствующие регистры АЛУ.
При сложении и вычитании сначала производится подготовительная операция, называемая выравниванием порядков.
| В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу. |
В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются.
В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу.
Пример 1. Сложить двоичные нормализованные числа 0.10111•2–1 и 0.11011*210. Разность порядков слагаемых здесь равна трем, поэтому перед сложением мантисса первого числа сдвигается на три разряда вправо:
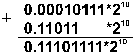
Пример 2. Выполнить вычитание двоичных нормализованных чисел 0.10101*210 и 0.11101*21. Разность порядков уменьшаемого и вычитаемого здесь равна единице, поэтому перед вычитанием мантисса второго числа сдвигается на один разряд вправо:
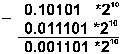
Результат получился не нормализованным, поэтому его мантисса сдвигается влево на два разряда с соответствующим уменьшением порядка на две единицы: 0.1101*20.
| При умножении двух нормализованных чисел их порядки складываются, а мантиссы перемножаются. |
Пример 3. Выполнить умножение двоичных нормализованных чисел:
| При делении двух нормализованных чисел из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя. Затем в случае необходимости полученный результат нормализуется. |
Пример 4. Выполнить деление двоичных нормализованных чисел:
Использование представления чисел с плавающей точкой существенно усложняет схему арифметико-логического устройства.
| [ следующий ] [ начало главы ] [ предыдущий ] | [ содержание ] |