[ следующий ] [ начало главы ] [ предыдущий ] [ содержание ]

7.10. Какие циклы называют итерационными?

Особенностью итерационного цикла является то,что число повторений операторов тела цикла заранее неизвестно. Для его организации используется цикл типа пока. Выход из итерационного цикла осуществляется в случае выполнения заданного условия.

На каждом шаге вычислений происходит последовательное приближение и проверка условия достижения искомого результата.

Пример. Составить алгоритм вычисления суммы ряда
 


с заданной точностью (для данного знакочередующегося степенного ряда требуемая точность будет достигнута, когда очередное слагаемое станет по абсолютной величине меньше).

Вычисление сумм — типичная циклическая задача. Особенностью же нашей конкретной задачи является то, что число слагаемых (а, следовательно, и число повторений тела цикла) заранее неизвестно. Поэтому выполнение цикла должно завершиться в момент достижения требуемой точности.

При составлении алгоритма нужно учесть, что знаки слагаемых чередуются и степень числа х в числителях слагаемых возрастает.

Решая эту задачу "в лоб" путем вычисления на каждом i-ом шаге частичной суммы
 

S:=S+(-1)**(i-1)*x**i/i ,

мы получим очень неэффективный алгоритм, требующий выполнения большого числа операций. Гораздо лучше организовать вычисления следующим образом: если обозначить числитель какого-либо слагаемого буквой р, то у следующего слагаемого числитель будет равен -р*х (знак минус обеспечивает чередование знаков слагаемых), а само слагаемое m будет равно p/i, где i - номер слагаемого.

Сравните эти два подхода по числу операций.
 
Алгоритм на школьном АЯ Блок-схема алгоритма 
 алг Сумма (арг вещ x, Eps, рез вещ S)
   дано | 0 < x < 1
   надо | S = x - x**2/2 + x**3/3 - ...
 нач цел i, вещ m, p
   ввод x, Eps
   S:=0; i:=1 | начальные значения
   m:=1; p:=-1
   нц пока abs(m) > Eps
     p:=-p*x | p - числитель
             | очередного слагаемого
     m:=p/i  | m - очередное слагаемое
     S:=S+m  | S - частичная сумма
     i:=i+1  | i - номер
             | очередного слагаемого
   кц
   вывод S
 кон

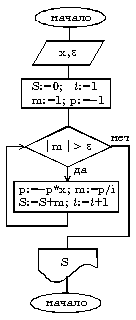Алгоритм, в состав которого входит итерационный цикл, называется итеpационным алгоpитмом. Итерационные алгоритмы используются при реализации итерационных численных методов.

В итерационных алгоритмах необходимо обеспечить обязательное достижение условия выхода из цикла (сходимость итерационного процесса). В противном случае произойдет зацикливание алгоритма, т.е. не будет выполняться основное свойство алгоритма — результативность.

[ следующий ] [ начало главы ] [ предыдущий ] [ содержание ]