Функции Эйри

Функции Эйри представляют собой независимые решения линейного дифференциального уравнения w"- zw = 0. В Mathematica эти функции представлены следующим набором:

AiryAi [z] — возвращает значение функции Эйри Ai(z);

AiryAiPrime [ z ] — возвращает значение производной функции Эйри Ai '(z);

AiryBi [z] — возвращает значение функции Эйри Bi(z);

AiryBiPrime [z] — возвращает производную функции Эйри Bi'(z).

Ниже представлены примеры на вычисление функций Эйри.

Ввод (In)	Вывод (Out)
AiryAi [2. +3.*I]	0.00810446 + 0.131178 I
AiryAi[l.]	0.135292
AiryBi [2. +3.*I]	-0.396368 - 0.569731 I
AiryBiPrime [2 . +3 . *I]	0.349458 - 1.10533 I

С функциями Эйри связаны многие специальные математические функции. Эта связь проявляется и при выполнении различных математических операций над функциями Эйри:

D[AiryAi[x],х]

AiryAiPrime[x]

Integrate[AiryBi[x],x]

{xGamma[1/3 ] HypergeometricPFQ[{1/3 }, {2/3,4/3}, x3/9]} /{3 31/6 Gamma [ 2/3 ] Gamma [ 5/3 ]}

{ x2Gamma[1/3 ] HypergeometricPFQ[{1/3 }, {2/3,4/3}, x3/9]} /{3 35/6 Gamma [ 4/3 ] Gamma [ 5/3 ]}

Series[AiryBi[x],{x,0,5}]

{1 /31/6xGamma[2/3]}+ {31/6x /Gamma[1/3]}+ {x3 /631/6Gamma[2/3]}+{x4 /435/6Gamma[1/3]}+O[x]6

Графики функций, Эйри представлены на рис. 6.11.

Нетрудно заметить, что при х < 0 они имеют колебательный характер.

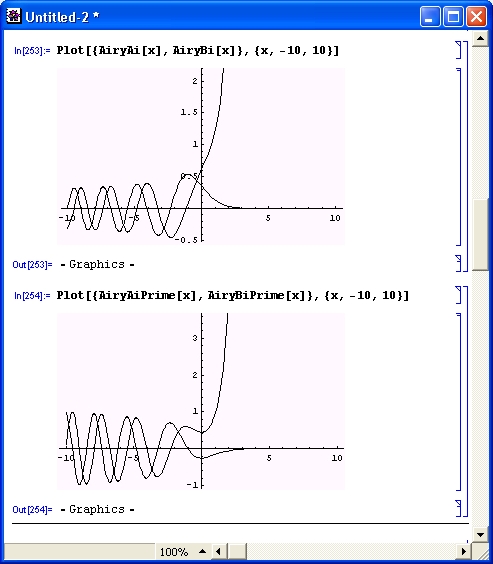
Рис. 6.11. Графики функций Эйри (сверху) и их производных (снизу)

Бета-функция и родственные ей функции

Класс бета-функций, имеющих специальное интегральное представление, в Mathematica представлен следующим набором:

Beta [а, b] — эйлерова бета-функция В(a, b);

Beta[z, а, b] — неполная бета-функция;

Beta[z0, zl, a, b] — обобщенная неполная бета-функция Beta [z1, a, b] - Beta[z0, а, b];

BetaRegularized [z, a> b] — регуляризированная неполная бета-функция I(z,a,b) = Betafz, a, b]/Beta[a, b];

BetaRegularized [z0, zl, a, b]—регуляризированная обобщенная неполная бета-функция I(z1l,a,b) - I(z0, a, b).

Поимепы на вычисление этих функций представлены ниже.

Ввод (In)	Вывод (Out)
Beta[l.,2.]	0.5
Beta[l.,2.,3.]	0.0833333
Beta[2.+3.I,4.+6.I,l,2]	4. - 12. I
BetaRegulari zed [0.1,1,2]	0.19