Специальные числа и полиномы

Для вычисления специальных чисел и полиномов служит следующая группа функций:

BernoulliB [n] — n-е число Бернулли;

BernoulliB [n, х] — полином Бернулли n-й степени;

Binomial [n, m] — биномиальный коэффициент;

Cyclotomic [n, х] — циклотомический полином порядка п по переменной х;

EulerE[n] — n-е число Эйлера;

EulerE[n, х] — n-й полином Эйлера;

EulerPhi [n] — эйлерова функция сумм ф(n) — количество положительных целых чисел, не превосходящих п и взаимно простых с и;

Fibonacci [n] — n-е число Фибоначчи;

Fibonacci [n, х] — полином Фибоначчи F _n (x);

Multinomial [n1, n2, . . . ] — мультиномиальный коэффициент (n! + n2 + . . .) !/(n1! n2! ...);

NBernoulliB [n] — численное значение n-го числа Бернулли;

NBernoulliB [n, d] — n-е число Бернулли с n?-цифровой точностью представления;

Pochhammer [а, n] — символ Похгамера;

StirlingSl [n, m] — число Стирлинга первого рода;

StirlingS2 [n, m] — число Стирлинга второго рода.

Ниже представлены примеры вычисления данных функций.

Ввод (In)	Вывод (Out)
N [BernoulliB [2]]	0.166667
BernoulliB [2, 0.1]	0.0766667
Binomial [6, 4]	15
Cyclotomic [ 5, х]	1 + x + x ² + x ³ + x ⁴
Cyclotomic [5,0.2]	1.2496
EulerE[2]	-1
EulerE[2,0.1]	-0.09
EulerPhi [2]	1
Fibonacci [10]	55
Fibonacci [ 6 , x]	3 x + 4 x ³ + x ⁵
Pochhammer [1,3]	6
StirlingSl [8, 4]	6769

На рис. 6.12 показаны графики полиномов Бернулли и циклотомического полинома различных порядков.

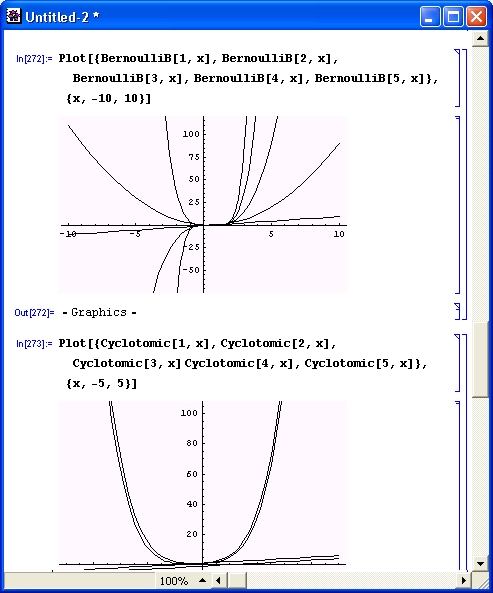
Рис. 6.12. Графики полиномов Бернулли (сверху) и циклотомических полиномов (снизу)

Обратите внимание на то, что здесь использована функция Plot, модифицированная пакетом расширения plot.m, который будет описан в уроке 10. Эта функция позволяет автоматически строить графики ряда функций с линиями разного стиля, что облегчает их распознавание.

На рис. 6.13 представлены графики полиномов Эйлера EulerE разного порядка п.

Помимо описанных выше, в ядро системы входит также ряд других, менее распространенных функций. Они описаны в приложении.

По числу встроенных специальных математических функций Mathemafica заметно превосходит другие системы компьютерной математики. При этом все такие функции могут участвовать в символьных преобразованиях. Это делает системы Mathematica предпочтительными при решении задач, в которых часто встречаются специальные математические функции. В то же время надо отметить, что многие специальные функции системами Mathemafica вычисляются только для целого порядка.

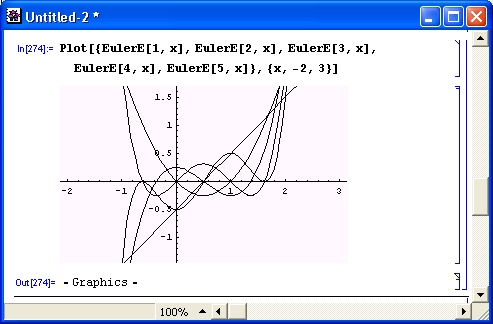
Рис. 6.13. Графики полиномов Эйлера разного порядка