2.6. Политропический процесс
В параграфе 2.4 отмечалось, что важным классом термодинамических процессов являются процессы, происходящие при постоянной теплоемкости, то есть политропические процессы. К таким процессам, в частности, относятся адиабатический, изотермический, изобарический и изохорический процессы.
Для идеального газа нетрудно получить уравнение политропического процесса тем же способом, которым ранее было выведено уравнение Пуассона. Пусть молярная теплоёмкость идеального газа в политропическом процессе равна 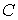 . Тогда в соответствии с первым началом термодинамики (1.5) имеем выражение:
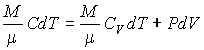 , , | (2.99) |
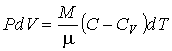 . . | (2.100) |
Подставляя это выражение в формулу (2.76) получим
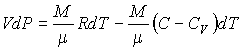 | (2.101) |
или с учетом соотношения Майера (2.70)
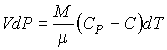 . . | (2.102) |
Сравнение формул (2.100) и (2.102) при условии, что 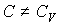 , позволяет записать уравнение
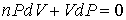 , , | (2.103) |
аналогичное уравнению (2.79). Здесь введен параметр
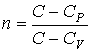 , , | (2.104) |
Из этой формулы можно также получить зависимость молярной теплоемкости 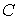 от показателя политропы 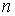 :
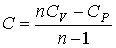 . . | (2.105) |
Преобразование формулы (2.103) к виду:
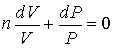 | (2.106) |
и интегрирование полученного уравнения дает
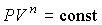 . . | (2.107) |
Аналогично уравнениям адиабаты (2.86) и (2.87) уравнение политропы может быть переписано в других термодинамических координатах:
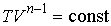 , , | (2.108) |
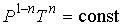 . . | (2.109) |
При адиабатическом процессе 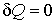 , что соответствует нулевой теплоемкости. Подставив 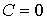 в формулу (2.104) и сравнив получившееся выражение с (2.80), имеем 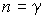 , и уравнение политропы (2.107) становится уравнением адиабаты: 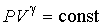 .
Если процесс изотермический, то 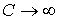 , так как при этом 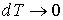 . В этом случае показатель политропы 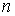 в пределе равен единице, и уравнение политропы (2.107) преобразуется в уравнение Бойля-Мариотта (2.11):  . Обратим внимание на то, что поскольку при выводе уравнения политропы мы исключали величину 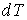 , то этот вывод не может считаться полностью корректным для изотермического процесса.
Для изобарического процесса при 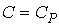 показатель политропы 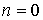 , и уравнение (2.107) принимает форму: 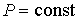 .
При изохорическом процессе 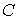 должно стать равным 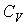 , что соответствует случаю, когда показатель 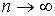 . Очевидно, переход в формуле (2.107) к указанному пределу некорректен. Это связано с тем, что при выводе уравнения политропы предполагалось, что 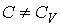 (см. переход к формуле (2.103)).
Если умножить уравнение (2.100) на величину 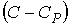 и сложить его с уравнением (2.102), предварительно умноженным на величину 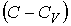 , то получим уравнение политропы в дифференциальном виде
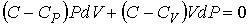 . . | (2.110) |
При 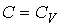 это уравнение приобретает форме:
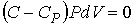 | (2.111) |
Отсюда имеем 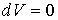 или 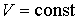 . Из уравнения (2.110) также следует, что в процессе, при котором 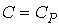 , давление постоянно: 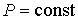 .
Для политропических процессов значение теплоёмкости и, соответственно, показателя политропы могут принимать любые величины. Отрицательные значения теплоёмкости, когда показатель политропы 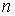 принимает значения от единицы до величины g (см. формулу (2.105)), соответствуют таким условиям, при которых внутренняя энергия термодинамической системы убывает при передаче ей положительного количества теплоты. Это может быть осуществлено при принудительном расширении газа.
В соответствии с формулой (2.100) при 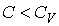 величины 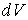 и 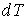 имеют различные знаки, и с ростом объёма газа его температура, а, следовательно, и внутренняя энергия, уменьшаются. С этим, в частности, связано понижение температуры идеального газа при его адиабатическом расширении, так как в этом процессе 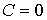 . Наоборот, при 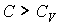 с ростом объёма газа его температура растёт. В соответствии с первым началом термодинамики этот рост должен быть обеспечен подводом к системе дополнительного количества теплоты.
Рассуждая аналогичным образом, можно на основании формулы (2.102) установить связь между приращениями давления и температуры. При 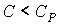 с ростом давления температура газа будет возрастать, а при 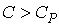 - уменьшаться.
Работа газа в политропическом процессе может быть определена с помощью интеграла (1.13) при подстановке в него уравнения политропы (2.107), аналогично тому, как это сделано в формуле (2.97):
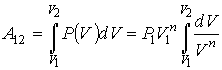 . . | (2.112) |
Интегрирование в выражении (2.112) дает формулу для определения работы в политропическом процессе
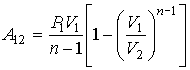 , , | (2.113) |
где: 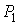 и 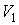 - начальные давление и объём газа, 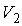 - его конечный объём.
Из этой формулы, в частности, следует, что работа при расширении газа всегда остаётся положительной, независимо от того, какое значение принимает показатель политропы, больше или меньше единицы.
Нетрудно видеть, что для адиабатического процесса при 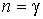 выражение (2.113) переходит в формулу (2.95). Для изобарического процесса, при 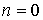 , выражение (2.113) дает
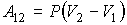 , , | (2.114) |
где учтено, что при этом процессе 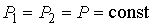 .
Формула (2.113) неприменима для описания изохорического процесса, так как при выводе уравнения политропы (2.103) исключался случай 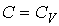 . Но из формулы (2.100) очевидно, что работа газа в изохорическом процессе равна нулю.
Другим процессом, не описывающимся соотношением (2.113), является изотермический процесс. Как было сказано выше, он является предельным случаем политропического процесса при 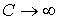 . Работу в изотермическом процессе можно найти, если в формулу (2.112) в соответствии с законом Бойля-Мариотта подставить 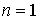 , а затем выполнить интегрирование. Тогда имеем
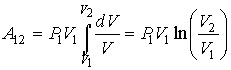 | (2.115) |
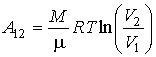 , , | (2.116) |
где учтено постоянство температуры в этом процессе: 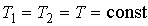 .
Поскольку внутренняя энергия идеального газа не изменяется в изотермическом процессе, количество теплоты, полученное газом, также может быть рассчитано по этой формуле, то есть в этом процессе 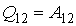 . При изотермическом расширении идеального газа работа совершается только за счёт теплоты, подведённой из окружающей среды.
В заключение параграфа запишем все полученные формулы в единую таблицу 2.1.
Термодинамический процесс | Показательполитропы | Теплоемкость | Работа |
Изотермический | 1 | | |
Изобарический | 0 | | |
Изохорический | | | 0 |
Адиабатический | | 0 | |
Задача 2.4. Какова молярная теплоёмкость 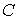 одноатомного газа и показатель политропы одноатомного газа и показатель политропы 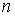 для процесса, в котором работа, совершаемая газом, в два раза превосходит количество теплоты, передаваемое ему? для процесса, в котором работа, совершаемая газом, в два раза превосходит количество теплоты, передаваемое ему?
Решение: Так как по условию задачи  , то в соответствии с первым началом термодинамики имеем: , то в соответствии с первым началом термодинамики имеем:
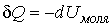 .
Тогда, с учетом одноатомности газа (число степеней свободы 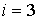 ), молярную теплоемкость можно определить по формуле: ), молярную теплоемкость можно определить по формуле:
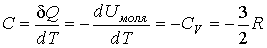 ,
а показатель политропы соответственно будет равен:
Задача 2.5. Какая работа совершается одним молем идеального газа в политропическом процессе с показателем политропы 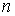 при изменении температуры газа на при изменении температуры газа на 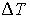 ? ?
Решение: Используя уравнение политропы (2.108): 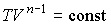 и уравнение Клапейрона-Менделеева для одного моля и уравнение Клапейрона-Менделеева для одного моля 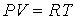 , перепишем (2.113) в виде: , перепишем (2.113) в виде:
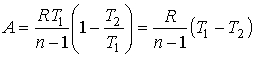 .
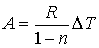 .
Следовательно, работа, совершаемая одном молем идеального газа в процессе с постоянной теплоёмкостью, определяется только разностью температур конечного и начального состояний газа.
Таким образом, для идеального газа работа, а, следовательно, и количество теплоты, в политропических процессах определяются только конечным и начальным состояниями системы, так как путь перехода из одного состояния в другое определён теплоёмкостью газа (показателем политропы). Однако даже при рассмотрении только политропических процессов, работу и количество теплоты нельзя считать функцией состояния системы, так как переход из одного состояния в другое может быть осуществлен последовательностью различных политропических процессов.
Задача 2.6. Какое количество теплоты передано одноатомному газу в процессе, описанному в условии задачи 2.5?
Решение: В соответствии с формулой (2.105) имеем:
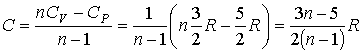 .
Тогда количество теплоты будет равно:
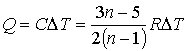 .
Отсюда, в частности, следует, что при равенстве показателя политропы показателю адиабаты для одноатомного газа: 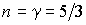 , количество теплоты , количество теплоты 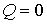 . .
|