| |
 |
| ГЛАВА 5. Статистическое описание равновесных состояний |
 |
|
 |
|
| |
 |
5.9. Статистическое обоснование второго начала термодинамики
Флуктуации, описание которых проведено в предыдущем параграфе, возникают в любых термодинамических системах. Для равновесных систем вероятность возникновения тех или иных флуктуаций зависит от их величины. Чем больше флуктуация, тем меньше вероятность ее возникновения.
Пусть имеется два одинаковых сосуда, соединенных между собой таким образом, чтобы газ из одного сосуда мог перетекать в другой. Находящийся в этих сосудах газ в равновесном случае равномерно распределится между этими сосудами, и вероятность нахождения каждой из молекул газа в любом из сосудов будет одинакова. Вследствие флуктуаций количество молекул газа в сосудах будет претерпевать хаотические изменения. При этом вероятность наблюдать то или иное состояние будет зависеть от того, насколько оно отличается от равновероятного. С увеличением отличия числа частиц в этих двух сосудах уменьшается вероятность возникновения такого состояния.
Пусть в начальный момент времени все молекулы газа находились в одном сосуде. Тогда по истечении некоторого времени произойдет перераспределение молекул, приводящее к возникновению равновесного состояния, характеризующегося равновероятным нахождением молекул в обоих сосудах. Самопроизвольный переход в исходное неравновесное состояние, при котором все молекулы сосредоточены в одном из сосудов, практически невозможен. То есть, обратный процесс перехода из равновесного в неравновесное состояние оказывается очень маловероятным.
Приведенный пример позволяет сделать вывод о том, что самопроизвольный переход из неравновесного состояния в равновесное является гораздо более вероятным, чем обратный переход. Этот вывод соответствует второму началу термодинамики, утверждающему, что термодинамическая система самопроизвольно переходит из неравновесного состояния в равновесное, а обратный процесс может происходить только при внешних воздействиях на систему.
Термодинамической величиной, характеризующей направление протекания самопроизвольных термодинамических процессов, является энтропия. В частности, переход в равновесное состояние адиабатически изолированной системы является более вероятным, чем обратный. И именно наиболее вероятному равновесному состоянию соответствует максимум значения энтропии.
Установим связь между величиной энтропии, соответствующей состоянию термодинамической системы, и вероятностью возникновения этого состояния. Пусть имеется некоторый сосуд, объемом 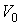 , внутри которого находится одна молекула. Будем считать, что вероятность нахождения молекулы в любом месте сосуда одинакова. Тогда вероятность того, что частица будет обнаружена внутри некоторого объема 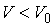 , выделенного внутри сосуда, равна: 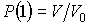 . Если в сосуде будет находиться не одна, а две частицы, то вероятность их одновременного нахождения в указанном объеме 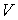 определяется как произведение вероятностей нахождения в этом объеме каждой из частиц: 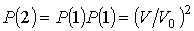 . Соответственно для 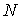 частиц, равновероятностно распределенных внутри сосуда, вероятность обнаружить их всех в объеме 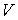 равна:
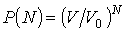 . . | (5.114) |
Пусть теперь в этом сосуде выделено два объема 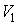 и 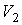 . Тогда, в соответствии с формулой (5.114), мы можем записать отношения вероятностей того, что все молекулы газа находятся в указанных объемах:
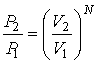 . . | (5.115) |
Определим приращение термодинамической энтропии в изотермическом процессе расширения идеального газа от состояния с объемом 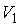 , до состояния с объемом 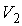 . Подстановка в формулу (3.53) выражения для передаваемой теплоты при изотермическом процессе
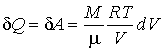 | (5.116) |
позволяет определить разность энтропий рассматриваемых состояний идеального газа:
 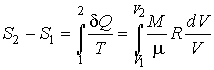 | (5.117) |
или после вычисления интеграла
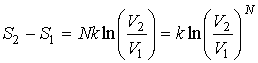 . . | (5.118) |
Здесь использовано соотношение: 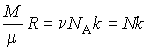 .
Подстановка формулы (5.115) в выражение (5.118) приводит его к окончательному виду:
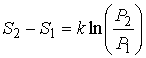 . . | (5.119) |
Как следует из этого выражения, переход термодинамической системы из состояния, имеющего меньшую вероятность, в состояние с большей вероятностью, ( 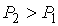 ) приводит к возрастанию энтропии.
Выражение (5.119) не определяет абсолютное значение энтропии в каком либо состоянии, а только дает возможность найти разность энтропий в двух различных состояниях. Для однозначного определения энтропии, удовлетворяющему третьему началу термодинамики, немецким физиком-теоретиком Максом Карлом Эрнестом Людвигом Планком (1858 - 1947) было предложено использовать вместо вероятности состояния 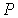 его статистический вес 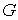 , величина которого выражается целыми положительными числами и пропорциональна вероятности: 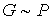 .
Если частицы системы могут с равной вероятностью 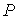 принимать некоторое количество 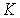 дискретных состояний и число частиц в системе равно 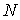 (для определенности будем считать 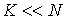 ), то соотношение между вероятностью 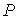 и статистическим весом 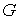 принимает вид:
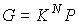 . . | (5.120) |
В наименее вероятном случае, когда все частицы сосредоточены в одном из дискретных состояний, статистический вес становится равным единице: 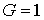 , а вероятность этого состояния соответственно равна: 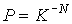 .
В более общем случае, если в 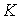 дискретных состояниях находятся соответственно 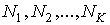 частиц, статистический вес 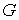 и вероятность 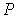 вычисляются по формулам:
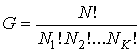 , , | (5.121) |
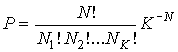 . . | (5.122) |
Здесь: 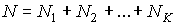 .
Переход к статистическому весу позволяет записать выражение для энтропии в следующем виде:
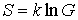 . . | (5.123) |
В частности, из этой формулы следует, что энтропия термодинамической системы со статистическим весом равным единице, когда все частицы системы находятся в одинаковых состояниях, равна нулю. А в состоянии с максимальным статистическим весом энтропия также принимает максимальное значение.
Для статистической энтропии выполняется требование аддитивности. Если система может быть разделена на две не взаимодействующие подсистемы, статистические веса которых соответственно равны 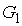 и 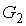 , то её статистический вес 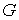 вычисляется как произведение весов подсистем: 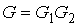 . При этом энтропия в соответствии с формулой (5.123) равна:
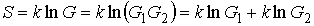 | (5.124) |
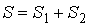 . . | (5.125) |
Согласно второму началу термодинамики, адиабатически изолированная термодинамическая система стремится к состоянию с наибольшим значением энтропии, а, следовательно, и с наибольшим значением статистического веса. Нахождение системы в таком состоянии имеет наибольшую вероятность. Отклонения от этого состояния возможны вследствие равновесных флуктуаций. Но после такого случайного отклонения система обязательно будет стремиться к наиболее вероятному равновесному состоянию.
В параграфе 3.9 мы уже указывали, что с законом возрастания энтропии связана гипотеза о тепловой смерти Вселенной. С точки зрения статистической теории тепловая смерть Вселенной - это такое её состояние, когда её статистический вес приобретает наибольшее значение. Такому состоянию соответствует Вселенная, в которой наблюдаются только равновесные флуктуации. Больцманом была высказана гипотеза о том, что наша Вселенная сейчас находится в состоянии гигантской флуктуации, и поэтому мы не наблюдаем сейчас её равновесного состояния. С течением времени Вселенная постепенно перейдет в равновесное состояние, которое вследствие случайных процессов, в какой-то момент времени может быть нарушено очередной гигантской флуктуацией.
Таким образом, представление Клаузиуса о тепловой смерти Вселенной как о состоянии полного отсутствия каких либо процессов, опровергается статистической теорией, допускающей существование во Вселенной достаточно больших флуктуаций, приводящих к постоянному течению в ней реально наблюдаемых природных процессов.
В заключение рассмотрим одно, предложенное Максвеллом, умозрительное устройство, которое, по его мнению, позволяло бы выводить изолированную термодинамическую систему из состояния равновесия без совершения работы и, соответственно, уменьшать её энтропию. Представим себе сосуд, разделенный перегородкой, через отверстие в которой могут пролетать частицы. Пусть это отверстие может перекрываться некоторой невесомой заглушкой, причем считаем, что механическая работа при этом не совершается. Предположим, что указанная заглушка открывается только тогда, когда из правой части сосуда в левую пытаются пролететь наиболее быстрые частицы и при пролетании из левой части в правую соответственно наиболее медленных частиц. Тогда через некоторое время в правой части сосредоточатся более медленные частицы, а в левой - более быстрые. Это приведет к тому, что среда, находящаяся в левой части нагреется, а среда в правой - охладится. Система приобретет неравновесное состояние, и её энтропия уменьшится. Возникшая разность температур может быть использована, в частности, для получения полезной работы с помощью тепловой машины.
При анализе работы рассматриваемого гипотетического устройства нами не был учтен факт получения информации о скорости частиц, что абсолютно необходимо для правильного определения моментов открывания и закрывания заглушки. А процесс получения информации является необратимым, и его протекание происходит с возрастанием энтропии и с затратами энергии. Поэтому суммарное изменение энтропии всей системы, включающей как сосуд с частицами, так и прибор для измерения скорости этих частиц, будет больше нуля в полном соответствии со вторым началом термодинамики.
Задача 5.6. Определить относительное изменение статистического веса при перехода одного моля одноатомного идеального газа из состояния с объемом 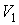 и температурой и температурой 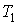 в состояние с объемом в состояние с объемом 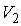 и температурой и температурой 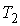 . .
Решение: В соответствии с формулой (4.18) изменение энтропии газа в рассматриваемом случае равно:
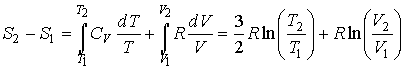 .
Подстановка в левую часть этой формулы вместо энтропии её выражения через статистический вес (формула (5.123)) дает:
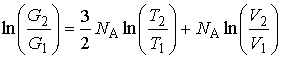 .
Окончательно получаем следующую формулу:
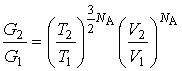 .
В частности, если в ходе рассматриваемого процесса температура и объем этого газа вырастут в два раза, то изменение статистического веса составит:
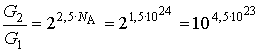 .
Получившееся относительное изменение статистического веса представляет собой очень большую величину.
|
 |
|
| |
 |
 |
| | |
|
 |
|
 |
 |
|
|