7.3. Явления на границе раздела газа, жидкости и твердого тела
Опыт показывает, что поверхность жидкости стремится принять такую форму, чтобы иметь минимальную площадь. Это явление связано с воздействием на поверхность жидкости механических сил, стремящихся уменьшить площадь этой поверхности. Указанные силы называются силами поверхностного натяжения.
Рассмотрим явления, возникающие на границе раздела жидкости и газа. Пусть имеется пленка жидкости (например, мыльная пленка), натянутая на рамку с одной подвижной перемычкой (см. рис. 7.1). | Рис. 7.1.
Рамка с жидкой пленкой |
За счет сил поверхностного натяжения пленка будет стремиться уменьшить свою площадь. Для того, чтобы воспрепятствовать этому, к перемычке необходимо приложить силу 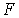 , величина которой, как показывает опыт, не зависит от площади пленки, а пропорциональна длине перемычки 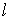 :
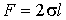 . . | (7.8) |
Коэффициент пропорциональности 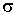 называется поверхностным натяжением ( коэффициентом поверхностного натяжения). Двойка в формуле (7.8) означает, что пленка жидкости имеет две поверхности и если её толщина много больше межмолекулярного расстояния, то происходит независимое воздействие двух поверхностей пленки на перемычку. Очевидно, что сила 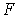 равна силе поверхностного натяжения и поэтому из формулы (7.8) следует, что величина силы поверхностного натяжения численно равна произведению поверхностного натяжения 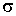 на длину линии контакта пленки и перемычки на длину линии контакта пленки и перемычки 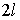 . Эта сила направлена по касательной к поверхности пленки.
При медленном перемещении перемычки на величину 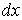 , площадь поверхности пленки увеличивается на величину
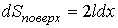 . . | (7.9) |
Требование медленности перемещения перемычки позволяет считать рассматриваемый процесс изотермическим и квазистатическим (обратимым).
С учетом выражения (7.8) элементарная работа 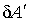 , которую необходимо совершить против сил поверхностного натяжения, определяется по формуле
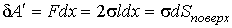 . . | (7.10) |
Соответственно работа 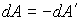 , совершаемая силами поверхностного натяжения примет вид
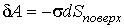 . . | (7.11) |
Существование свободной поверхностной энергии обусловлено силами притяжения между молекулами жидкости. В результате действия этих сил молекулы поверхностного слоя втягиваются внутрь жидкости, в то время как для молекул, расположенных внутри жидкости, равнодействующая сил притяжения равна нулю. Аналогичное явление имеет место в газе Ван-дер-Ваальса (см. параграф 2.7), что приводит к уменьшению давления этого газа на стенки сосуда. В жидкости силы межмолекулярного притяжения также приводят к изменению давления на её поверхность.
Для преодоления действия межмолекулярных сил над молекулой газа необходимо совершить работу, которую надо затратить на перемещение этой молекулы из объема жидкости на её поверхность. Величина этой работы численно равна приращению потенциальной энергии молекулы жидкости, которая и обуславливает появление сил поверхностного натяжения. Поскольку число молекул в приповерхностном слое пропорционально его площади, то суммарная потенциальная энергия всех молекул (свободная поверхностная энергия) также пропорциональна площади поверхности.
Состояние равновесия жидкости, в отсутствие сил гравитационного притяжения и других внешних сил, имеет место при минимальной площади поверхности, соответствующей заданному объему жидкости. Этим объясняется то, что в невесомости капля жидкости принимает шарообразную форму. Мыльный пузырь имеет почти сферическую форму вследствие малости своего веса.
Рассмотрим теперь явления, происходящие с каплей жидкости, помещенной на поверхность твердого тела. В этом случае имеются три границы раздела между фазами: газ-жидкость, жидкость-твердое тело и газ-твердое тело. Поведение капли жидкости будет определяться значениями поверхностного натяжения (удельными величинами свободной поверхностной энергии) на указанных границах раздела. Сила поверхностного натяжения на границе раздела жидкости и газа будет стремиться придать капле сферическую форму. Это произойдет в том случае, если поверхностное натяжение на границе раздела жидкости и твердого тела будет больше поверхностного натяжения на границе раздела газа и твердого тела (см. рис. 7.2(а)). В этом случае процесс стягивания жидкой капли в сферу приводит к уменьшению площади поверхности границы раздела жидкость-твердое тело при одновременном увеличении площади поверхности границы раздела газ-жидкость. Тогда наблюдается несмачивание поверхности твердого тела жидкостью. Форма капли будет определяться равнодействующей сил поверхностного натяжения и силы тяжести. Если капля большая, то она будет растекаться по поверхности, а если маленькая - стремиться к шарообразной форме. | Рис. 7.2.
Различные формы капли на поверхности твердого тела для случаев несмачивающей (а) и смачивающей (б) жидкостей |
Если поверхностное натяжение на границе раздела жидкости и твердого тела меньше поверхностного натяжения на границе раздела газа и твердого тела, то капля приобретет такую форму, чтобы уменьшить площадь поверхности границы раздела газ-твердое тело, то есть будет растекаться по поверхности тела (см. рис. 7.2(б)). В этом случае наблюдается смачивание жидкостью твердого тела.
Для количественного описания смачивания жидкостью твердого тела рассмотрим равновесие сил, действующих на элемент 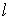 контура, образованного пересечением трех границ раздела фаз: газа 1, жидкости 2 и твердого тела 3 (см. рис. 7.3). | Рис. 7.3.
Схемы к расчету равновесия капли на поверхности твердого тела для случаев несмачивающей (а) и смачивающей (б) жидкостей
1 - газ, 2 - жидкость, 3 - твердое тело |
Для случая механического равновесия имеем
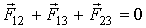 , , | (7.12) |
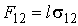 , , | (7.13) |
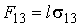 , , | (7.14) |
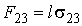 , , | (7.15) |
а величины 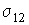 , 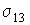 и 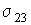 - равны поверхностному натяжению на границах раздела газ-жидкость, газ-твердое тело и жидкость-твердое тело.
В проекции на горизонтальную ось формулы (7.12) - (7.15) позволяют записать условие равновесия (см. рис 7.3)
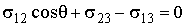 , , | (7.16) |
где проведено сокращение на величину длины элемента контура 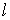 .
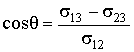 . . | (7.17) |
Как следует из этой формулы, равновесию жидкости на поверхности твердого тела соответствует вполне определенный угол 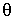 , который называется краевым углом. Этот угол может принимать значения от 0 до  .
Так как 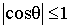 , то из формулы (7.17) следует условие существования устойчивого равновесия жидкости на поверхности твердого тела:
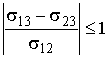 . . | (7.18) |
Если это условие не выполняется, капля либо, при
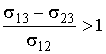 , , | (7.19) |
начинает неограниченно (до толщины нескольких мономолекулярных слоев) растекаться по поверхности, либо, при
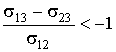 , , | (7.20) |
Явление смачивания (или несмачивания) твердого тела жидкостью приводит к появлению капиллярного эффекта. Капилляром называется тонкая трубка, вставленная в сосуд с жидкостью. Капиллярный эффект связан с тем, что в зависимости от того, смачивает жидкость стенки капилляра или нет, внутри капилляра поверхность жидкости приобретает соответственно вогнутую или выпуклую форму. В первом случае давление внутри жидкости уменьшается по сравнению с внешним, и она поднимается внутри капилляра (см. рис. 7.4(а)). А во втором - это давление возрастает, что приводит к опусканию уровня жидкости в капилляре по отношению к её уровню в сосуде (см. рис. 7.4(б)). | Рис. 7.4.
Капилляр в смачивающей (а) и не смачивающей (б) жидкостях |
Подъем жидкости в капилляре и дополнительное давление могут быть определены из условия минимума потенциальной энергии 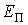
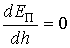 , , | (7.21) |
где: 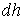 - элементарное изменение высоты столба жидкости в капилляре.
Для повышения уровня жидкости в цилиндрическом капилляре на величину 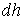 необходимо совершит работу против сил тяжести
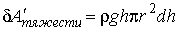 | (7.22) |
и сил поверхностного натяжения
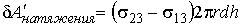 . . | (7.23) |
Здесь: 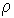 - плотность жидкости, 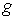 - ускорение свободного падения, 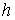 - высота подъема жидкости в капилляре, 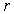 - радиус капилляра, 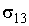 и 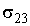 - поверхностное натяжение на границе раздела газа и капилляра, и жидкости и капилляра соответственно. Тогда изменение энергии
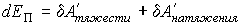 | (7.24) |
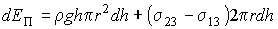 . . | (7.25) |
Таким образом, условие (7.21) приобретает вид
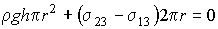 . . | (7.26) |
Учет формулы (7.17) позволяет записать последнее выражение в форме
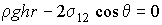 , , | (7.27) |
где: 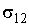 - поверхностное натяжение на границе раздела газа и жидкости. Отсюда следует, что высота подъема жидкости в капилляре определяется выражением
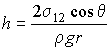 . . | (7.28) |
Из этой формулы следует, что при 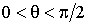 уровень жидкости в капилляре повышается, а при 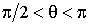 - соответственно понижается.
Так как дополнительное давление 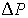 , создаваемое поверхностью жидкости должно уравновешиваться гидростатическим давлением, то имеем
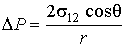 | (7.29) |
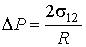 , , | (7.30) |
Теоретическое описание явления поверхностного натяжения может быть осуществлено с помощью метода термодинамических потенциалов, рассмотренного в параграфе 4.2. В первой главе нами было получено выражение (1.12), позволяющее определить механическую работу, которая совершается при движении границы раздела жидкости и газа. Однако это выражение не учитывает работу сил межмолекулярного взаимодействия (сил поверхностного натяжения), которая необходима для создания единицы площади поверхности раздела фаз. Учет этой работы (см. формулу (7.11)) приводит к следующему выражению для полной механической работы, совершаемой при движении границы раздела
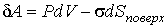 , , | (7.31) |
где величина 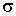 описывает поверхностное натяжение на границе раздела фаз.
Тогда, с учетом работы сил межмолекулярного взаимодействия, в формулу (4.35) для дифференциала свободной энергии (термодинамического потенциала Гельмгольца) 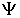 необходимо добавить новое слагаемое, которое описывает вклад поверхностного натяжения:
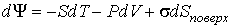 . . | (7.32) |
Как следует из этого выражения, при описании поверхностного натяжения площадь поверхности 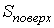 является таким же параметром состояния, как и объем 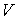 .
Пусть имеется система, состоящая из жидкости, описываемой параметрами 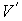 и 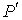 , газа, с параметрами 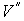 и  , и границы их раздела. Будем считать, что общий объем жидкости и газа постоянен: 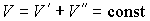 , и их температуры одинаковы: 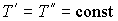 . Тогда дифференциал 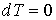 , и для такой системы дифференциал свободной энергии 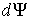 принимает вид:
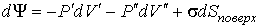 . . | (7.33) |
В условиях равновесия 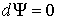 имеем
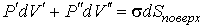 . . | (7.34) |
Так как 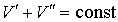 , то 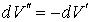 . Тогда выражение (7.34) можно преобразовать к виду:
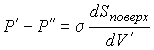 . . | (7.35) |
Если поверхность сферическая, то 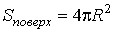 , 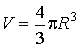 и, следовательно:
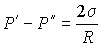 . . | (7.36) |
В случае, если поверхность имеет произвольную форму и характеризуется двумя главными радиусами 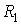 и 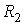 , то:
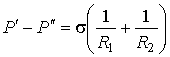 . . | (7.37) |
Выражение (7.37) является обобщением формулы Лапласа (7.36) на случай произвольной формы поверхности жидкости (см. также формулу (7.30)). При 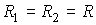 выражение (7.37) переходит в (7.36).
Если поверхность жидкости имеет цилиндрическую форму, то один из радиусов в формуле (7.37) становится бесконечным, и для этого случая формула (7.37) приобретает вид
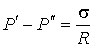 , , | (7.38) |
где: 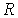 - радиус цилиндрической поверхности жидкости.
Термодинамический потенциал Гельмгольца (7.32) позволяет также определить зависимость поверхностного натяжения 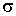 от температуры 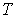 . Будем считать, что давление жидкости 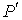 и газа 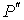 поддерживаются одинаковыми: 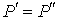 . Тогда с учетом того, что 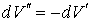 имеем выражение для свободной энергии в виде:
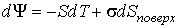 . . | (7.39) |
Из этого выражения следует
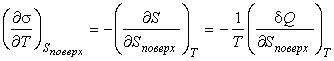 . . | (7.40) |
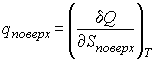 , , | (7.41) |
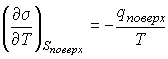 . . | (7.42) |
Как показывает опыт, теплота изотермического образования единицы поверхности 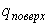 является положительной величиной. Поэтому поверхностное натяжение 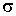 уменьшается с повышением температуры, причем быстрота этого уменьшения обратно пропорциональна абсолютной температуре.
Задача 7.1. Найти силу притяжения двух квадратных пластинок, между которыми находится слой жидкости, толщиной 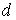 . Размер пластинок . Размер пластинок 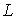 много больше толщины слоя жидкости. Коэффициент поверхностного натяжения жидкости равен много больше толщины слоя жидкости. Коэффициент поверхностного натяжения жидкости равен 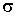 . Считать, что жидкость полностью смачивает пластинки. . Считать, что жидкость полностью смачивает пластинки.
Решение: В соответствии с формулой Лапласа (7.38) для случая цилиндрической формы поверхности жидкости имеем выражение для разности атмосферного давления и давления внутри жидкости:
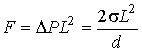 .
По мере уменьшения толщины слоя жидкости, величины 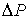 и и 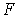 растут, и это приводит к тому, что капля жидкости стремится максимально растечься между пластинами. Минимальная толщина слоя жидкости будет определяться степенью параллельности поверхностей пластинок и качеством их обработки. Чем лучше отшлифованы пластинки, тем сильнее они притягиваются. Для случая воды, находящейся между стеклянными пластинками, разность давлений может достигать величины атмосферного давления. растут, и это приводит к тому, что капля жидкости стремится максимально растечься между пластинами. Минимальная толщина слоя жидкости будет определяться степенью параллельности поверхностей пластинок и качеством их обработки. Чем лучше отшлифованы пластинки, тем сильнее они притягиваются. Для случая воды, находящейся между стеклянными пластинками, разность давлений может достигать величины атмосферного давления.
Отметим, что, несмотря на достаточно большую силу притяжения пластинок, их можно легко рассоединить, сдвигая друг относительно друга вдоль плоскости поверхности.
Задача 7.2. Найти радиус 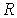 пузырька газа, находящегося в воде при температуре пузырька газа, находящегося в воде при температуре 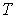 с поверхностным натяжением с поверхностным натяжением 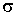 , если величина гидростатического давления воды , если величина гидростатического давления воды 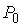 , а концентрация молекул газа равна , а концентрация молекул газа равна 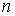 . Пузырек считать сферическим, а газ - идеальным. . Пузырек считать сферическим, а газ - идеальным.
Решение: Согласно формуле Лапласа (7.36), давление газа в сферическом пузырьке равно
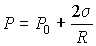 .
В соответствии с основным уравнением молекулярно-кинетической теории (см. формулу (2.32))
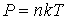 .
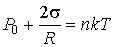 .
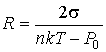 .
Очевидно, что давление газа в пузырьке больше гидростатического давления воды на величину давления, создаваемого поверхностным натяжением.
|